Question

The angle of elevation of the top of a tower 30m high from the foot of another tower in the same plane is ${60^ \circ }$ and the angle of elevation of the top of the second tower from the foot of the first tower is ${30^ \circ }$. Find the height of the other tower.

Answer 1

Hint:
We will solve this question by using the trigonometric function $\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$ in the right triangles, one by one, obtained by sketching the given conditions. We will calculate the value of the base common to both the triangles and then we will put the value of base to calculate the value of the height of the second tower.

Complete step by step solution:
We are given that the angle of elevation of the top of a tower whose height is 30m from the foot of the other tower is ${60^ \circ }$.
The angle of elevation of the top of the second tower from the foot of the other tower is ${30^ \circ }$.
We need to find the height of the second tower.
The figure of this given question will be:

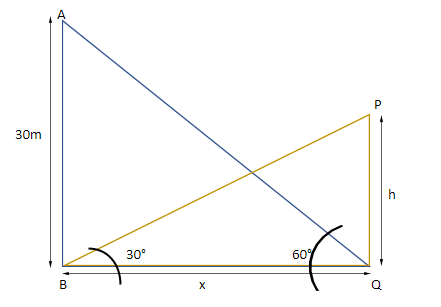
Let AB be the first tower and PQ be the second tower with height h. The angle of elevation of the first tower AB from the foot of the second tower PQ is $\angle AQB = {60^ \circ }$. The angle of elevation of the second tower PQ from the foot of the first tower AB is$\angle PBQ = {30^ \circ }$ .
Applying the trigonometric identity $\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$ in $\vartriangle ABQ$ ,
$
   \Rightarrow \tan {60^ \circ } = \dfrac{{30}}{x} \\
   \Rightarrow \sqrt 3 = \dfrac{{30}}{x} \\
   \Rightarrow x = \dfrac{{30}}{{\sqrt 3 }} \\
 $
Applying $\tan \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$ in the $\vartriangle PBQ$ ,
$ \Rightarrow \tan {30^ \circ } = \dfrac{h}{x}$
Substituting the value of x in the above equation, we get
$
   \Rightarrow \tan {30^ \circ } = \dfrac{h}{{\left( {\dfrac{{30}}{{\sqrt 3 }}} \right)}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{h\sqrt 3 }}{{30}} \\
   \Rightarrow h = \dfrac{{30}}{3} = 10m \\
 $

Therefore, the height of the second tower is 10m.

Note:
In this question, you may go wrong in understanding the setup and hence constructing the diagram to get a clear view and also in the use of the calculation of the x to calculate the value of the height of the tower. This question is a part of a major concept, Trigonometry, of mathematics which is widely used in real – life. We measure heights of big monuments and buildings, depth of the sea and many more other spaces of life where heights and distances are involved.