Question

The angle of elevation of the top of a hill from the foot of a tower is \[{{60}^{\circ }}\] and the angle of depression from the top of the tower to the foot of the hill is \[{{30}^{\circ }}\]. If the tower is 50m high, find the height of the hill.

Answer 1

- Hint: In this question, we first need to draw the diagram with the given conditions which gives us a clear picture of what we have to find. Then assume the height of the hill as some variable and then using the tangent formula we can get the result.
\[\tan \theta =\dfrac{\text{opposite}}{\text{adjacent}}\]


Complete step-by-step solution -

Let us first draw the diagram with the given conditions in the question

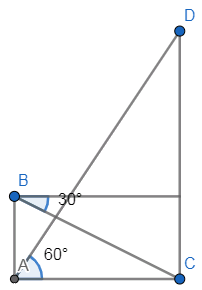
Now, given in the question that
\[\begin{align}
  & AB=50 \\
 & \angle DAC={{60}^{\circ }} \\
\end{align}\]
Now, from the given angle of depression we can also write that
\[\angle BCA={{30}^{\circ }}\]
Let us assume that the height of the hill as x
\[CD=x\]
Let us also assume the distance between the bottom points of the hill and tower as y.
\[AC=y\]
As we already know the tangent values for some of the standard angles we get,
\[\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}} \\
 & \tan {{60}^{\circ }}=\sqrt{3} \\
\end{align}\]
Now, by applying the tangent formula to the triangle ACD we get,
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{CD}{AC}\]
Now, on substituting the respective values in the above equation we get,
\[\Rightarrow \sqrt{3}=\dfrac{x}{y}.......\left( 1 \right)\]
Now, by applying the tangent formula to the triangle ABC we get,
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{AB}{AC}\]
Now, on substituting the respective values in the above equation we get,
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{50}{y}\]
Now, by doing cross multiplication in the above equation we get,
\[\therefore y=50\times \sqrt{3}\]
Now, by substituting this value of y in the above equation (1) we get,
\[\begin{align}
  & \Rightarrow \sqrt{3}=\dfrac{x}{y} \\
 & \Rightarrow \sqrt{3}=\dfrac{x}{50\times \sqrt{3}} \\
\end{align}\]
Now, on further cross multiplication of the terms in the above equation we get,
\[\begin{align}
  & \Rightarrow x=\sqrt{3}\times 50\times \sqrt{3} \\
 & \Rightarrow x=50\times 3 \\
 & \therefore x=150m \\
\end{align}\]
Hence, the height of the hill is 150m.


Note: Instead of assuming some variable y to the base distance AC we can directly calculate it. It is also important to note that instead of finding the value of y and then again substituting back in the equation to get the value of x we can directly get x by dividing both the equations obtained by the tangent formula.
On dividing both the equations obtained by the tangent formula the common term base distance which is AC gets cancelled directly and then by further simplification we can directly get the value of x.
While cross multiplying and rearranging the terms we should not neglect any of the terms because it changes the corresponding equation and so the final result.