Question

The angle of elevation of the top of a $24m$ high pillar from the window of a building $6m$ above the ground and the angle of depression of its base are complementary angles. The distance of the building from the pillar is
A) $2\sqrt 3 m$
B) $8\sqrt 3 m$
C) $12\sqrt 3 m$
D) $6\sqrt 3 m$

Answer 1

Hint: We can draw a diagram with the given details. Then we can find 2 right angles triangle. Then we can form 2 trigonometric ratios with the complementary angles with the known height and the required distance. Then we can eliminate the complementary angles using the relation $\tan \left( {90^\circ - a} \right) = \cos a$ and basic trigonometric relations. We can solve the equation to get the required distance.

Complete step by step solution: We can draw a figure for better understanding.

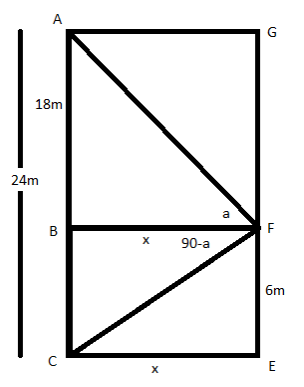
According to the figure, AC is the tower of height 24m, FE is the height of the window of the building and $CE = BF = x$ is the distance of the building from the pillar. Then $\angle AFB = a$ is the angle of elevation and $\angle BFC$ is the angle of depression.
From the question, we are given that both angles are complementary. So, if $\angle AFB + \angle BFC = 90^\circ $,
$
   \Rightarrow \angle BFC = 90^\circ - \angle AFB \\
   \Rightarrow \angle BFC = 90^\circ - a \\
 $
Now consider the right triangle, ABF,
$\tan \angle AFB = \dfrac{{AB}}{{BF}}$
$ \Rightarrow \tan a = \dfrac{{18}}{x}$… (1)
Now we can consider the right-angled triangle CBF,
$
  \tan \angle BFC = \dfrac{{BC}}{{BF}} \\
   \Rightarrow \tan \left( {90^\circ - a} \right) = \dfrac{6}{x} \\
 $
We know that $\tan \left( {90^\circ - a} \right) = \cot a$and $\cot a = \dfrac{1}{{\tan a}}$.
$ \Rightarrow \dfrac{1}{{\tan a}} = \dfrac{6}{x}$… (2)
Substituting (1) in (2) we get.
$\dfrac{x}{{18}} = \dfrac{6}{x}$
We can cross multiply the equation.
$ \Rightarrow {x^2} = 6 \times 18$
On taking the positive square root, we get,
$
  x = \sqrt {6 \times 6 \times 3} \\
   \Rightarrow x = 6\sqrt 3 \\
 $
So, the distance of the building from the pillar is $6\sqrt 3 $

Therefore, the correct answer is option D.

Note: When we look at an object above our eye level, our line of sight will make an angle with the horizontal eye level. This angle is called the angle of elevation. If we are at the top of some building or a tower and we look at some object below our eye level. Then the angle that the line of sight makes with the horizontal eye level is called the angle of depression.

We use the concept of trigonometry to solve this problem. Drawing a diagram with the given details is important to understand the question. Complementary angles are the angles that give sum of $90^\circ $.