Question

The angle of elevation of an aeroplane from a point A on the ground is ${{45}^{\circ }}$. After flight of 15 seconds the angle of elevation changes to ${{30}^{\circ }}$. If the aeroplane is flying at a constant height of 3000m find the speed of the plane in km/hr.

Answer 1

Hint: In this question, we are given the angle of elevation of an aeroplane at two different time intervals and we have to find the speed of the plane. For this, we will first draw a diagram to understand the question clearly. Using diagrams we will find the distance covered by plane. Since we are given time and distance is found, so we will use $\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$ formula to calculate required speed. For converting speed from meter per second to kilometers per hour, we will multiply the answer by $\dfrac{18}{5}$. In triangles formed, we will use following formula:
\[\tan \theta =\dfrac{\text{side opposite to angle }\theta }{\text{side adjacent to angle }\theta }\]

Complete step by step answer:
Let us first draw a diagram using a statement of question to simplify our understanding.

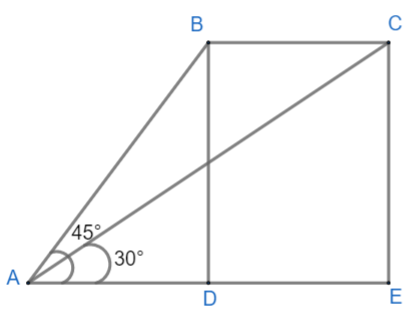
Here, aeroplane is flying at a constant height of 3000m, so BD = CE = 3000m from point A, angle of elevation was ${{45}^{\circ }}$ therefore, $\angle BAD={{45}^{\circ }}$. Aeroplane moved distance BC in 15 seconds and the angle of elevation changes to ${{30}^{\circ }}$. Therefore $\angle CAD={{30}^{\circ }}$. Hence, we have obtained two right angled triangles $\Delta ABD\text{ and }\Delta ACE$.
We have to find distance BC so that we can calculate speed.
In triangle ADB, $\angle BAD={{45}^{\circ }}$
As we know, \[\tan \theta =\dfrac{\text{side opposite to angle }\theta }{\text{side adjacent to angle }\theta }\]
Therefore, in $\Delta ADB$, $\tan {{45}^{\circ }}=\dfrac{BD}{AD}$.
As calculated earlier, BD = 3000m and we know $\tan {{45}^{\circ }}=1$. Therefore, $1=\dfrac{3000}{AD}$.
Cross multiplying we get: AD = 3000m
Now in triangle CAE,
$\tan {{30}^{\circ }}=\dfrac{CE}{AE}$.
Since CE = 3000m and we know $\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}$ therefore, we get:
$\dfrac{1}{\sqrt{3}}=\dfrac{3000}{AE}$.
Cross multiplying we get: $AE=3000\times \sqrt{3}m$.
Now, we need to find BC. As we can see from diagram BC = DE, therefore let us calculate DE.
Since, DE = AE - AD.
Therefore, let us put the value of AE and AD obtained earlier to find the value of DE. Hence,
$DE=\left( 3000\sqrt{3}-3000 \right)$.
Therefore, distance covered by plane in 15 seconds $\Rightarrow \left( 3000\sqrt{3}-3000 \right)$.
Now we know distance as well as time. So, we can calculate speed using formula:
$\text{Speed}=\dfrac{\text{Distance}}{\text{Time}}$.
Therefore, $\text{Speed}=\dfrac{\text{3000}\left( \sqrt{3}-1 \right)}{\text{15}}=146.41\text{ mtr/sec}$.
Now, converting it to km/hr, let's multiply it with $\dfrac{18}{5}$ so we get:

$\text{Speed}=146.41\times \dfrac{18}{5}=527.04km/hr$.

Note: Students should note that, multiplying by $\dfrac{18}{5}$ is a shortcut to convert meter/second to km/hr. They can also convert it using normal metric measures like $146.41\times \dfrac{60\times 60}{1000}=527.04km/hr$. Here $60\times 60$ describes the number of seconds in an hour and 1000 describes meters in a kilometer. Students should always draw diagrams for these kinds of sums. Students should not get confused in writing units.