Question

The angle of elevation of a cloud from a point h meters above the surface of a lake is $\theta $ and the angle of depression of its reflection in the lake is $\varnothing $ . Prove that the height of the cloud above the lake surface is :$h\left( \dfrac{\tan \varnothing +\tan \theta }{\tan \varnothing -\tan \theta } \right)$

Answer 1

Hint: Draw the figure assuming cloud and viewer as 2 points. All the distance between all represented by straight lines. You will find 2 triangles. Take elevation, depression as given in the question. By using the definition of tangent, find the tangent of both of them in terms of side lengths. By using the condition that horizontal distance is the same equate the terms, you get for horizontal distance in both equations. By this you get a relation between angles, which is the required result in the question.

Complete step-by-step answer:
Tangent of angle:- Tangent of angle in a triangle is defined as ratio of side opposite to the angle to the side length which is adjacent to the angle. Let us take angle x in triangle ABC. Then tan x is:

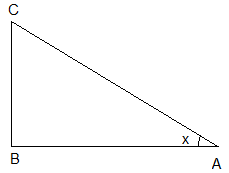
$\tan x=\dfrac{BC}{AB}$
Given conditions in the question all written as:

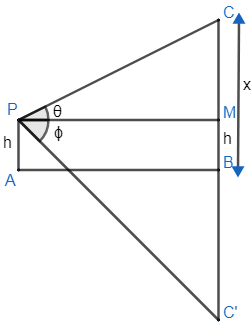
View point is h m above the lake. Clouds are at $\theta $ elevation. Reflection of cloud is at $\varnothing $ depression.
Point P is a viewer and Point C is cloud, A, B lake.
Assume the cloud is at x m from the lake surface.
By definition of tangent, we can say that –
$\tan \theta =\dfrac{CM}{PM}$
As the cloud is at x m as per assumption at viewer is at h m. So, $CB=x,MB=h$
By diagram we can say the relation between them as:$CM=CB-MB$
By substituting them, we can get value of CM as –
$CM=x-h$
By substituting this into above equation of angles, we get $\tan \theta =\dfrac{x-n}{PM}$
By cross multiplication, we get value of PM as:
$PM=\dfrac{x-h}{\tan \theta }$ ……………………….. (1)
By definition of tangent on depression, we get it as:
$\tan \varnothing =\dfrac{C'M}{PM}$
As C’ is reflection of C in AB (lake) , we get:
$C'B=CB$
By substituting its value, we get the equation as:
$C'B=x$
By diagram we can say the relation given by:
$C'M=C'B+BM$
By substituting the values, we get the equation as:
$C'M=x+h$
By substituting this in tangent equation, we get it as:
$\tan \varnothing =\dfrac{x+h}{PM}$
By cross multiplication, we can say its value to be as:
$PM=\dfrac{x+h}{\tan \varnothing }$ ……………………… (2)
By equating the equations (1) and (2), we get it as:
$\dfrac{x-h}{\tan \theta }=\dfrac{x+h}{\tan \varnothing }$
By cross multiplication we get it in the form of:
$\left( x-h \right)\tan \varnothing =\left( x+h \right)\tan \theta $
By distributive law, we get it in the form of:
$x\tan \varnothing -h\tan \varnothing =x\tan \theta +h\tan \theta $
By combining similar terms together, we get it as:
$x\tan \varnothing -x\tan \theta =h\tan \varnothing +h\tan \theta $
By taking x, h common, we can write it in form of:
$x\left( \tan \varnothing -\tan \theta \right)=h\left( \tan \varnothing +\tan \theta \right)$
By simplifying, we get the final value of x as:
$x=\dfrac{h\left( \tan \varnothing +\tan \theta \right)}{\left( \tan \varnothing -\tan \theta \right)}$
X is the distance of the cloud from lake surface.
Hence, we proved.

Note: Do not forget to consider that the viewer is h m above lake. Or else you will get the wrong answer. While taking tangents do not confuse. Always opposite sides must be in numerator students confuse and write adjacent sides in numeration. But it is wrong. The idea of $x+h,x-h$ is bought because we need sum, difference of tangents of elevation depression. This is a very crucial idea. So, handle it carefully.