Question

The angle of elevation of a cloud from a point \[60m\] above a lake is \[{30^ \circ }\] and the angle of depression of the reflection of the cloud in the lake is \[{60^ \circ }\]. Find the height of the cloud from the surface of the lake.

Answer 1

Hint: The question requires us to find the height of the cloud which is equivalent to finding the side of a triangle by drawing a diagram. We will be also required to use the trigonometric identities to solve the given question since the angle of elevation is \[{30^ \circ }\].

Complete step-by-step answer:
Let us draw a diagram for better understanding:

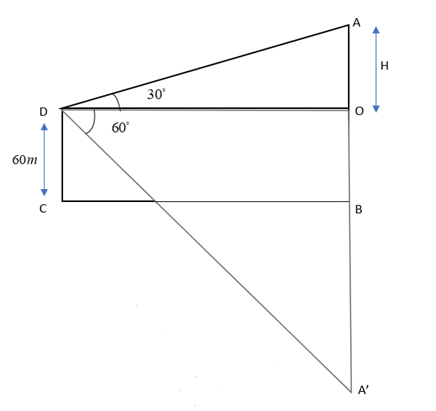
Here we draw the points with \[\overline {CB} \]as base of the lake.
The angle of elevation of cloud from a point \[60m\] is \[{30^ \circ }\]. Hence, we draw \[\vartriangle AOD\]with \[m\angle D = {30^ \circ }\].
\[\overline {CD} \] has a height of \[60m\].
Now since the angle of depression of the reflection of cloud is \[{60^ \circ }\], we draw \[\vartriangle DOA'\] with \[m\angle D = {60^ \circ }\]passing through point \[B\] in \[\square OBCD\] in downward location as shown in diagram.
Now we have to find the height of cloud from surface of the lake i.e. \[\overline {A'A} \].
Let \[\overline {AO} = H\]
\[ \Rightarrow A'B = AB = (60 + H)m\]
Here \[CD = OB = 60m\] since \[\square OBCD\]is a rectangle with equal opposite sides.
Now in \[\vartriangle AOD\], applying trigonometric identities,
\[\tan {30^ \circ } = \dfrac{{AO}}{{OD}} = \dfrac{H}{{OD}}\]
With the help of trigonometric ratio table, we get \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}\]
Substituting the value as per above, we get,
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{H}{{OD}}\]
\[H = \dfrac{{OD}}{{\sqrt 3 }}\]
\[OD = \sqrt 3 H\]
Now in \[\vartriangle DOA'\]. Applying trigonometric identities,
\[\tan {60^ \circ } = \dfrac{{OA'}}{{OD}} = \dfrac{{OB + A'B}}{{OD}}\]
With the help of trigonometric ratio table, we get \[\tan {60^ \circ } = \sqrt 3 \]
Substituting the value as per above, we get,
\[\sqrt 3 = \dfrac{{60 + (60 + H)}}{{\sqrt 3 H}}\]
\[\sqrt 3 = \dfrac{{120 + H}}{{\sqrt 3 H}}\]
Solving the equation, we get,
\[3H = 120 + H\]
\[2H = 120\]
\[H = 60\]
Now the height of cloud from surface of lake will be:
\[AB = 60 + H\]\[120m\]
\[AB = 60 + 60\]
\[AB = 120\]
Hence the height will be .

Note: We have used tangent as trigonometric identity since we have to find the opposite side of the angle with the information about adjacent side. The meaning of tangent is given below for better understanding:
The ratio of side opposite to given angle and its adjacent side is called tangent. It is denoted as \[\tan \theta \].
\[\tan \theta = \dfrac{{Side\,opposite\,to\,given\,angle}}{{Side\,adjacent\,to\,given\,angle}}\]