Question

The angle of elevation of a cloud from a point 60 meters above the lake is $30{}^\circ $ and the angle of depression of the reflection of the cloud in the lake is $60{}^\circ $. Find the height of the cloud from the surface of the lake.

Answer 1

Hint: We will draw a rough diagram to understand what is being asked in the question. We will use the definition of the trigonometric function, $\tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}}$ and the values of the trigonometric function for the angles $30{}^\circ $ and $60{}^\circ $. Using these, we will find the height of the cloud from the surface of the lake.

Complete step-by-step solution
Let us draw a rough diagram to understand the given question.

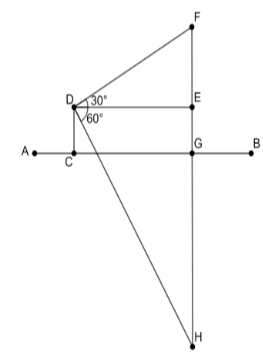
According to our figure, we know that point F is the cloud, segment AB is the lake, and $\text{CD = 60 meters }$. Point H is the reflection of the cloud in the lake. We have to find the height of the cloud from the surface of the lake, which is the length of segment GF. We can see that $\text{GF = GE + EF}$ and $\text{GE = CD = 60}$. Also, $\text{GF = GH}$ because H is the reflected image of the cloud.
Now, let us consider $\Delta \text{EDF}$. The angle of elevation at point D is given to be $30{}^\circ $. Hence, $\angle \text{EDF = 30}{}^\circ $. From the figure, we can see that $\angle \text{FED = 90}{}^\circ $. In $\Delta \text{EDF}$, let us look at $\tan 30{}^\circ $.
We know that $\tan \theta =\dfrac{\text{Opposite}}{\text{Adjacent}}$ and $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$. So, we get the following,
$\dfrac{1}{\sqrt{3}}=\dfrac{\text{EF}}{\text{ED}}$
Therefore, $\text{ED = }\sqrt{3}\cdot \text{EF}$.
Next, we will consider $\Delta \text{DEH}$. The angle of depression at point D is given as $60{}^\circ $, that is $\angle \text{EDH = 60}{}^\circ $. From the figure, we can see that $\angle \text{DEH = 90}{}^\circ $. Again, we will look at the trigonometric function $\tan $ for $\angle \text{EDH}$. So, we get
$\tan 60{}^\circ =\dfrac{\text{EH}}{\text{ED}}$
Now, we know that $\tan 60{}^\circ =\sqrt{3}$ and $\text{EH = GE + GH}$. Substituting these values in the above expression, we get
$\sqrt{3}=\dfrac{\text{GE + GH}}{\text{ED}}$
We know that $\text{ED = }\sqrt{3}\cdot \text{EF}$, $\text{GE = 60}$ and $\text{GF = GH}$ and also $\text{GF = GE + EF}$. Substituting these values in the above equation, we get the following,
$\sqrt{3}=\dfrac{\text{60 + 60 + EF}}{\sqrt{3}\cdot \text{EF}}$
Solving the above equation, we obtain
$\begin{align}
  & 3\cdot \text{EF}=120\text{ + EF} \\
 & \Rightarrow 2\cdot \text{EF = 120} \\
 & \therefore \text{EF = 60 metres} \\
\end{align}$
Hence, the height of the cloud from the surface of the lake is
$\text{GF = GE + EF = 60 + 60 = 120 metres}$.

Note: It is essential that we understand the concept of angle of elevation and angle of depression. It is always useful to draw rough diagrams for this type of question. The calculations become easier if we are familiar with the definitions of trigonometric functions and their values for standard angles. It is necessary that we label the diagram and use these labels while mentioning the segments so that we can avoid any confusion.