Question

The angle of elevation of a cloud from a point 60m above a lake is ${30^ \circ }$ and the angle of depression of the reflection of cloud in the lake is ${60^ \circ }$.Find the height of the cloud from sea level.

Answer 1

Hint:
In this problem we are going to make a diagram first and then take trigonometric relations in different right triangles. Firstly we consider the given problem step by step and try to make a diagram for finding the height of cloud for sea level. In this we will use the formula of trigonometric ratios. And the formula is given below.

Formula Used:
Since In this question we need the trigonometric ratio of $\tan \theta $ which is equal to $\dfrac{P}{B}$, where P is the perpendicular and B is base of the respective right angled triangle we use in it.

Complete step-by-step answer:
First we have to make a diagram. The steps for making the diagram are given below.

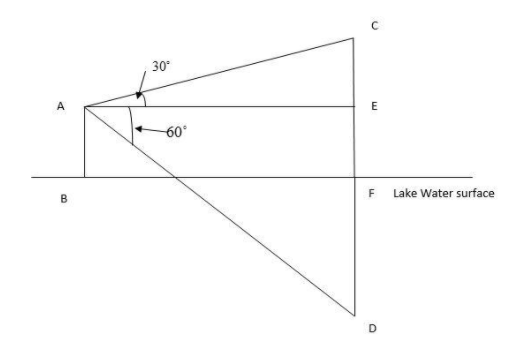
In the diagram let us consider AB is equal to the height of point from sea level and CF is the height of cloud where angles of elevation and depression are marked in above diagram.
Now we are going to calculate the height of cloud, As per the given data AB = 60 m
In the diagram, C is the point of the cloud.
CF is the height of cloud from surface of water
Now let us assume the height of the cloud be h metre.
So,
Let CF = h m
In the diagram FD is the shadow of cloud in water
Since the length of the FD will be same as of CF as FD is reflection of CF we get,
So, FD = reflection height of cloud =h m.
In the diagram, triangle BEC and BED are right angled triangles
Now the height of the point from lake level is 60 m which is also equal to the EF in diagram
We get, EF = AB =60 m
Now, we apply the use of trigonometric ratio in below triangles
Now, in triangle BEC
We are going to use trigonometric ratios, here we use $\tan \theta $ which is equal to the $\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}$as stated above

$\tan {\text{B = }}\dfrac{{{\text{Side opposite to angle B}}}}{{{\text{Side adjacent to angle B}}}}$
From the triangle BEC we will find the perpendicular is CE and Base is BE.
Let us put the values of perpendicular and base in above expression we get,
Since in triangle BEC the angle B is the angle of elevation which is${30^ \circ }$
So we get,
$\tan {30^ \circ } = \dfrac{{{\text{CE}}}}{{{\text{BE}}}}$ Where the angle of elevation is ${30^ \circ }$
Since, we know that$\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$, Values of the trigonometric ratios at specific angles
From the figure we can identify ${\text{CE = h - 60}}$ on substituting the known values in equation we get,
\[\dfrac{1}{{\sqrt 3 }} = \dfrac{{{\text{h - 60}}}}{{{\text{BE}}}}\]
Now we cross multiply the above expression therefore we get,
\[{\text{BE = }}\sqrt 3 \left( {{\text{h - 60}}} \right){\text{m}}\] ----- [1]
Similarly in right triangle BED
Perpendicular is ED and base is BE as shown in diagram and the angle B is the angle of depression which is given ${60^ \circ }$in problem
Putting the values we get
\[\tan {60^ \circ } = \dfrac{{{\text{ED}}}}{{{\text{BE}}}}\]Where angle of Depression is ${60^ \circ }$
We are going to use the value of $\tan {60^ \circ } = \sqrt 3 $as trigonometric ratios of specific angles in diagram${\text{ED = h + 60}}$
By substituting the values in equation we get,
$\sqrt 3 = \dfrac{{{\text{h + 60}}}}{{{\text{BE}}}}$
We Cross multiply on above equation, we get,
$\sqrt 3 {\text{BE = h + 60}}$……[2]
Now, we have \[{\text{BE = }}\sqrt 3 \left( {{\text{h - 60}}} \right){\text{m}}\]from [1]
We are going to substitute it in the equation (2) we get
$\sqrt 3 \times \sqrt 3 \left( {{\text{h - 60}}} \right) = {\text{h + 60}}$
By solving the above equation we get,
${\text{3h - 180 = h + 60}}$
 We are going to add both sides by –h and 180 we get from above equation,
$2{\text{h = 240}}$
Dividing both sides by 2 we get,
${\text{h = 120 m}}$
So, the height of the cloud = 120m.
Hence the height of cloud from sea level is coming out to be 120 m.

Note:
Be careful while marking the angle of elevation and depression because the change in marking would change the whole problem.