Question

The angle of elevation of a cloud from a point 100 meter above the surface of a lake is ${30^0}$ and the angle of depression of its image in the lake is ${60^0}$ then the height of the cloud above the lake is:
A) 100 m
B) 50 m
C) 200 m
D) 150 m

Answer 1

Hint: In order to solve the problem; first of all draw a pictorial representation of the problem statement. Then use the concept of heights and distance along with trigonometric identities and the values for trigonometric terms at some particular angle in order to proceed.

Complete step-by-step answer:

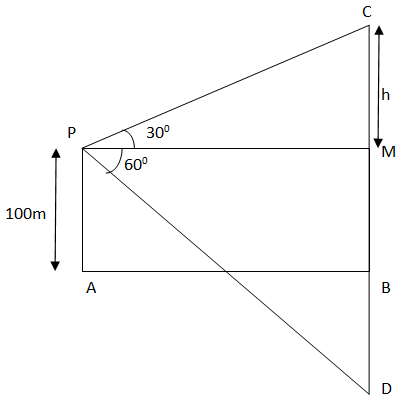
Let us use the following figure to solve the problem.

Let AB be the surface of the lake and P be the point of observation such that AP = 100 m.

Let C be the position of the cloud and D be its reflection in the lake.

Then as AB is the surface of the lake. So \[CB = BD\]

Let CM = h meter, then $CB = h + 100\& DB = h + 100$

In right $\Delta CMP$

\[

  \tan {30^0} = \dfrac{{CM}}{{PM}} \\

   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{PM}}{\text{ }}\left[ {\because \tan {{30}^0} = \dfrac{1}{{\sqrt 3 }}\& CM = h} \right] \\

   \Rightarrow PM = \sqrt 3 h.............(1) \\

 \]

Also in right $\Delta PMD$

\[

  \tan {60^0} = \dfrac{{DM}}{{PM}} \\

   \Rightarrow \sqrt 3 = \dfrac{{DB + BM}}{{PM}}{\text{ }}\left[ {\because \tan {{30}^0} = \dfrac{1}{{\sqrt 3 }}} \right] \\

   \Rightarrow \sqrt 3 = \dfrac{{h + 100 + 100}}{{PM}}{\text{ }}\left[ {DB = h + 100\& BM = 100} \right] \\

   \Rightarrow PM = \dfrac{{h + 200}}{{\sqrt 3 }}.............(2) \\

 \]

Now let equate equation (1) and equation (2) in order to find the value of h

$

   \Rightarrow \sqrt 3 h = \dfrac{{h + 200}}{{\sqrt 3 }} \\

   \Rightarrow \sqrt 3 \times \sqrt 3 h = h + 200 \\

   \Rightarrow 3h = h + 200 \\

   \Rightarrow 2h = 200 \\

   \Rightarrow h = \dfrac{{200}}{2} \\

   \Rightarrow h = 100m \\

 $

Now as we have the height h or CM as well as BM.

In order to find the height of the cloud above the surface of the lake, let us add the height of CM and BM.

Height of the cloud above the surface of lake:

$

   \Rightarrow CB = CM + BM \\

   \Rightarrow CB = h + 100 = 100 + 100 \\

   \Rightarrow CB = 200m \\

 $

Hence, the height of the cloud above the lake is 200 meter.

So, option C is the correct option.

Note: In order to solve such questions related to the concept of heights and distances the figure plays the most important role so the problem must be started with the figure. Also the students must remember the values of trigonometric functions of some important angles as they are used several times.