Question

The angle of deviation when light is incident at an angle of $45{}^\circ $ on one of the refracting faces of an equilateral prism of refractive index 1.414 is
$\begin{align}
  & \text{A}\text{. 40}{}^\circ \\
 & \text{B}\text{. 30}{}^\circ \\
 & \text{C}\text{. 45}{}^\circ \\
 & \text{D}\text{. 50}{}^\circ \\
\end{align}$

Answer 1

Hint: By using the formula of refractive index for prism, we get the correct answer. The angle of deviation of a ray of light passing through a prism depends upon its material as well as on the angle of incidence. Here it means it depends upon the refractive index of a material of prism.

Complete answer step by step:
The given prism is equilateral so the three angles are of \[60{}^\circ \]. So, $\angle A=60{}^\circ $.

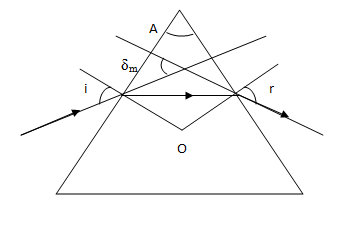
The angle of incident is given,

$\angle i=45{}^\circ $

We know that the equation for refractive index of prism,

\[\mu =\dfrac{\sin \left[ \dfrac{A+{{\delta }_{m}}}{2} \right]}{\sin \left( \dfrac{A}{2} \right)}\]
where µ is the refractive index of prism and ${{\delta }_{m}}$ is angle of deviation.
Substituting given values in above equation we get,

\[1.414=\dfrac{\sin \left[ \dfrac{60{}^\circ +{{\delta }_{m}}}{2} \right]}{\sin \left( \dfrac{60{}^\circ }{2} \right)}=\dfrac{\sin \left[ \dfrac{60{}^\circ +{{\delta }_{m}}}{2} \right]}{\sin \left( 30{}^\circ \right)}\]

We know \[\sin \left( 30{}^\circ \right)=\dfrac{1}{2}=0.5\], so above equation can be written as,

\[1.414\times 0.5=\sin \left[ \dfrac{60{}^\circ +{{\delta }_{m}}}{2} \right]\]
\[0.707=\sin \left[ \dfrac{60{}^\circ +{{\delta }_{m}}}{2} \right]\]

Multiplying both sides by ${{\sin }^{-1}}$, we get

\[{{\sin }^{-1}}(0.707)=\left[ \dfrac{60+{{\delta }_{m}}}{2} \right]\]
We know, \[\sin \left( 45{}^\circ \right)=\dfrac{1}{\sqrt{2}}=0.707\], so above equation can be written as,

\[\begin{align}
  & 45{}^\circ =\dfrac{60{}^\circ +{{\delta }_{m}}}{2} \\
 & \Rightarrow {{\delta }_{m}}=45{}^\circ \times 2-60{}^\circ \\
\end{align}\]

\[{{\delta }_{m}}={{30}^{0}}\]

Therefore, the angle of deviation when light is incident at an angle of $45{}^\circ $ on one of the refracting faces of an equilateral prism of refractive index 1.414 is \[{{\delta }_{m}}={{30}^{0}}\]

Hence the correct option is B.

Note: The given prism is equilateral, so the angle of the prism is known and also the angle of incidence is given with the refractive index of the prism. Here, Snell’s equation is used and substituted values of ‘i' and ‘r’. And they are \[i=\dfrac{A+{{\delta }_{m}}}{2}\] and \[r=\dfrac{A}{2}\].
So, if we know which material is used and what is the angle of incident, we can solve any problem of prism.