Question

The angle of depression of a boat from the top of a cliff 300m high is \[{60^ \circ }\]. The distance of the boat from the foot of the cliff is
(a) \[100\sqrt 3 \]
(b) 100
(c) \[300\sqrt 3 \]
(d) 300

Answer 1

Hint: To solve the question given above, first we will find out what is the angle of depression. Then, we will draw the rough sketch from the information provided in the question. Then, by applying trigonometry in the triangle formed, we will calculate the value of distance from the boat.
Complete step by step solution:
Before solving the question, we must know what is an angle of depression. An angle of depression is the downward angle from the horizontal to a line of sight from the observer to some point of interest. In the question, it is given that the angle of depression is \[{60^ \circ }\] . The height of the cliff is 300m. Thus, we will draw the rough sketch first. The rough sketch is as follows:

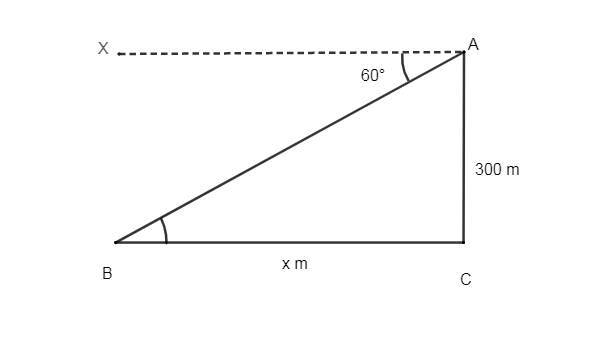
From the above figure, we can see that the height of the cliff is \[ = AC = 300m\] . We have assumed that the distance of the boat from the foot of the cliff is \['x'\,m\]. Also, we have drawn XA parallel to the horizontal line BC and AC is perpendicular to BC. Thus, the triangle ABC is a right angled triangle. Now \[\angle ABC = \angle XAB\] because they are alternate interior angles \[\left( {XA\parallel BC} \right)\] . So \[\angle ABC = {60^ \circ }\] . Now, we will consider the triangle ABC. In triangle ABC, we have:
\[\begin{array}{l}{\rm{tan}}\left( {\angle ABC} \right) = \dfrac{{AC}}{{BC}}\\ \Rightarrow {\rm{tan}}\left( {\angle ABC} \right) = \dfrac{{300}}{x}\\ \Rightarrow {\rm{tan}}\,\,{60^ \circ } = \dfrac{{300}}{x}\\ \Rightarrow x = \dfrac{{300}}{{{\rm{tan}}\,\,{{60}^ \circ }}}\end{array}\]
The value of \[{60^ \circ }\] is \[\sqrt 3 \] . So, we have the following equation:
\[x = \dfrac{{300}}{{\sqrt 3 }}\]
Now, we will rationalize the term on right hand side:
\[\begin{array}{l} \Rightarrow x = \dfrac{{300}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\ \Rightarrow x = \dfrac{{300\sqrt 3 }}{3}\\ \Rightarrow x = 100\sqrt 3 \\ \Rightarrow BC = 100\sqrt 3 \end{array}\]
Hence, option (a) is correct.

Note: While solving the above equation, we have made two assumptions. One assumption is that the cliff is perfectly perpendicular to the horizontal and the second assumption is that the boat and the cliff lies on the same horizontal line i.e. BC is horizontal and it is not inclined at any angle to horizontal.