Question

The angle of depression of a boat B from the top K of a cliff HK \[300\] metres high is \[30^\circ \]. Find the distance of the boat from the foot H of the cliff.
1) \[300\sqrt 3 \]m
2) \[400\sqrt 3 \]m
3) \[500\sqrt 3 \]m
4) \[600\sqrt 3 \]m

Answer 1

Hint: We will use trigonometric ratios to find the solution. The angle of depression is calculated using the formula \[\tan \theta = \dfrac{{oppositeside}}{{adjacentside}}\]. We will use a similar formula to find the required distance of the boat from the cliff.

Complete step-by-step answer:

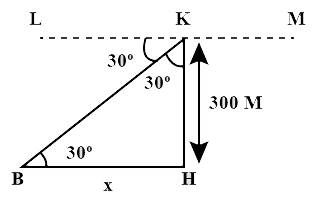
We know that the angle of depression is formed when the observer is higher than the object he/she is looking at and that the angle is dependent on two factors, height and distance.
Let us take the required distance \[BH = x\]metres.
By looking at the figure, we observe that \[HK\]is the cliff and \[\angle LKB\]is the angle of depression of B from K.
The height of the cliff is given to be \[300\]metres.
We know that when two lines are parallel then the alternate angles are equal to each other.
So, since\[LM\parallel BH\],
\[\angle KBH = \angle LKB = 30^\circ \] [Alternate angles]
Therefore, in \[\Delta KBH\],
\[
  \tan 30^\circ = \dfrac{{KH}}{{BH}} \\
   \Rightarrow \tan 30^\circ = \dfrac{{300}}{x} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{300}}{x} \\
   \Rightarrow x = 300\sqrt 3 \\
\]
We use \[\tan 30^\circ \]because we know that the angle of depression is calculated by \[\tan \theta = \dfrac{{oppositeside}}{{adjacentside}}\], so we simply use the same formula to find the distance which is the adjacent side and the height of the cliff is the opposite side to \[\angle KBH\].
Therefore, the distance of the boat from the foot H of the cliff is \[300\sqrt 3 \]m.
Thus, the answer is option A.

Note: We need to remember that whenever we are asked problems regarding the angle of depression or the angle of elevation, we will have to use trigonometric ratios, mainly \[\tan \theta \], to find the solution.