Question

The angle measures of $x$ and $y$ are respectively

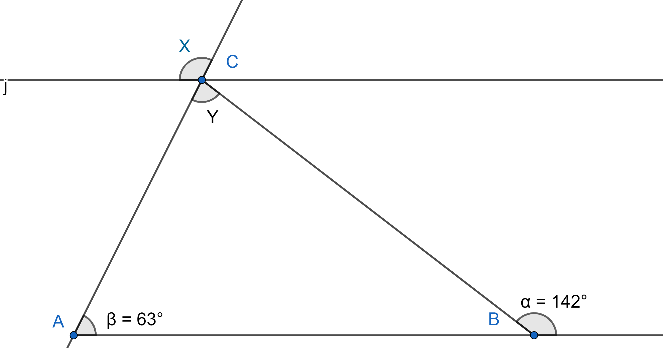
A) ${{63}^{\circ }},{{142}^{\circ }}$
B) ${{113}^{\circ }},{{38}^{\circ }}$
C) ${{117}^{\circ }},{{79}^{\circ }}$
D) ${{115}^{\circ }},{{75}^{\circ }}$

Answer 1

Hint: To solve this question we need to know the relation between the angles formed in the triangle. The angle formed on the straight line is ${{180}^{\circ }}$. The property of corresponding angle is also used to solve the problem. The sum of angles of a triangle is ${{180}^{\circ }}$.The transversal line is the line which cuts the two parallel lines given.

Complete step by step solution:
The question asks us to find the angles $x$ and $y$ in the given triangle. On analysing the figure given below we can see that line $AB$ is parallel to line $j$. Since these two lines are parallel lines $AC$ and line $BC$ are transversal on the parallel lines. Transversal line refers to the line which cuts the two parallel lines.

We will start with finding the angle$\angle Y$. We are aware of the fact that the sum of angles in the triangle is equal to ${{180}^{\circ }}$. On writing it mathematically we get:
$\angle ABC+\angle BCA+\angle CAB={{180}^{\circ }}$ ……………(i)
We can see in the figure $\angle CBA$ is not given. Instead the outer angle is given. So here we can apply the property that the angle made by straight line is ${{180}^{\circ }}$,so applying the same we get:
$\angle ABC+\alpha ={{180}^{\circ }}$
$\Rightarrow \angle ABC={{180}^{\circ }}-\alpha$
$\Rightarrow \angle ABC={{180}^{\circ }}-{{142}^{\circ }}={{38}^{\circ }}$
On substituting the values in equation (i), we get:
$\Rightarrow {{38}^{\circ }}+Y+{{63}^{\circ }}={{180}^{\circ }}$
$\Rightarrow Y+{{101}^{\circ }}={{180}^{\circ }}$
$\Rightarrow Y={{180}^{\circ }}-{{101}^{\circ }}$
$\Rightarrow Y={{79}^{\circ }}$
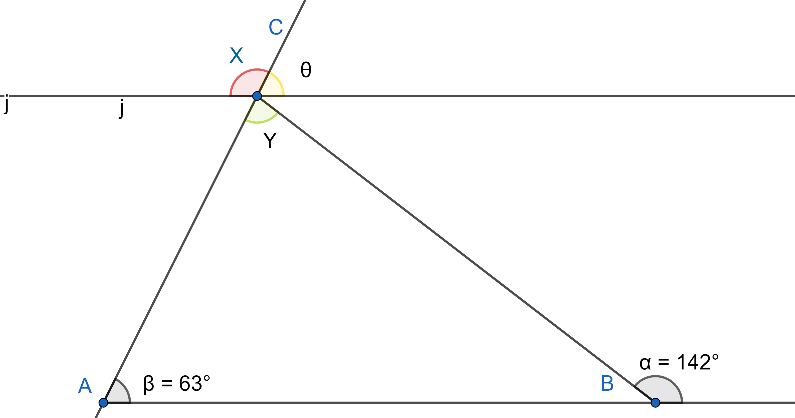
Now we will find the angle $\angle x$ . We know that the lines are parallel and AC is the transversal on the two parallel lines. Angle$\theta $ and angle $x$ are on the same line so their sum will result in ${{180}^{\circ }}$. Mathematically it would be written as:
$x+\theta ={{180}^{\circ }}$
To find angle $\theta $ we need to know the property of angles in case of parallel lines and transversal. So angle $\theta $ and angle $\beta $ are equal because both are corresponding angles.
$\Rightarrow \beta =\theta ={{63}^{\circ }}$
Substituting the value of $\theta $ we get:
$\Rightarrow x+{{63}^{\circ }}={{180}^{\circ }}$
$\Rightarrow x={{180}^{\circ }}-{{63}^{\circ }}$
$\Rightarrow {{117}^{\circ }}$
So, the correct answer is “Option C”.

Note: All the properties of the triangle should be known to us to solve the value for the angles. Angle $\angle Y$ could also be found by applying the exterior angle property. This means :$\angle CAB+\angle ACB=\alpha $
On putting the values we get:
$\Rightarrow {{63}^{\circ }}+Y={{142}^{\circ }}$
$\Rightarrow Y={{142}^{\circ }}-{{63}^{\circ }}$
$\Rightarrow Y={{79}^{\circ }}$
So the method can also be used to find the angle of the triangle if the opposite exterior angle is given.