Question

The angle in one regular polygon is to that in another as 3:2; also the number of sides in the first is twice that in the second; how many sides have the polygons?

Answer 1

Hint: First find a formula for an interior angle in an n – sided polygon. Now you get a relation between angle and number of sides. So by using the first condition you can derive an equation in terms of the number of sides of both the polygons. By using the second condition. Now you have 2 equations in 2 variables, so by applying a substitution method you can get the values of 2 variables. Thus, getting the values of the number of sides.

Complete step-by-step solution
As we know all angles (interior) are equal in a regular polygon we can write interior angle = $\dfrac{\text{Sum of all interior angles}}{n} -------(1)$. So, now we need the sum of all interior angles.

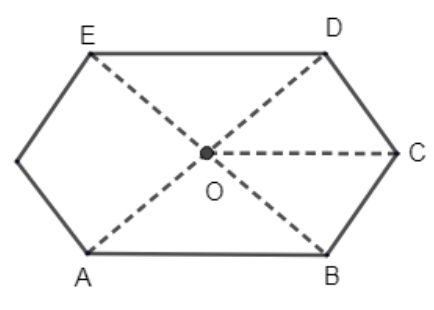
Let us take an “n” – sided polygon ABCDE. Take any point O inside and join OA, OB, OC,…… For n sided polygon, we get n triangles. We know the sum of triangles is \[{{180}^{\circ }}\]. So, the sum of angles of n triangles is \[n\times {{180}^{\circ }}\].
From the above statement, we can say that the angles as:
Sum of all interior angles + Sum of angles at O = \[n\times {{180}^{\circ }}\].
By diagram, we can say: Sum of angles at O = \[{{360}^{\circ }}\].
By substituting this and subtracting 360 on both sides we get,
Sum of all interior angles = \[n\times 180-360\].
By substituting this in equation (1) we get:
Interior angle of polygon = \[\dfrac{180n-360}{n}\] ----- (2)
From the question the 2 conditions, we have been given as:
The ratio of angles of both polygons is 3:2 ------ (3)
The number of sides of the first is twice that of the second ------- (4)
First, let us assume the angle of the first polygon as x and the number of sides of this are m.
Next, let us assume the angle of the second polygon as y and the number of sides of this is n.
From condition (3), we can write it as:
\[\Rightarrow x:y=3:2\]
By converting the ratio into a fraction, we get them as:
\[\Rightarrow \dfrac{x}{y}=\dfrac{3}{2}\] ---------(5)
From condition (4), we can write the relation between sides as:
\[\Rightarrow m=2n\] -------------(6)
From equation (2), we get a relation between x, m as:
\[\Rightarrow x=\dfrac{180m-360}{m}\] ----------- (7)
From equation (2), we can get a relation between y, n as:
\[\Rightarrow y=\dfrac{180n-360}{n}\] --------- (8)
By substituting equation (7), equation (8) into equation (5), we get:
\[\Rightarrow \dfrac{\dfrac{180m-360}{m}}{\dfrac{180n-360}{n}}=\dfrac{3}{2}\]
By simplifying the left-hand side, we can write it as:
\[\Rightarrow \dfrac{180mn-360n}{180mn-360m}=\dfrac{3}{2}\]
By taking 180 commons from numerator, denominator, and canceling we get:
\[\Rightarrow \dfrac{mn-2n}{mn-2m}=\dfrac{3}{2}\]
By cross multiplying the equation, we get it as follows:
\[\Rightarrow 2mn-4n=3mn-6m\]
By simplifying the terms, we get the equation as:
\[\Rightarrow mn-6m+4n=0\] ------------ (9)
Now we have 2 variables, 2 equations systems. So, we use a substitution method.
 Substitution method:
 First write 2 curve equations, which you need to solve to find intersection points. Then try to convert one variable in terms of another variable by using any one of the equations. Now substitute this variable in terms of others into the remaining equation. Now the remaining equation turns into an equation of one variable.
By substituting equation (6) into equation (9), we get:
\[\Rightarrow \left( 2n \right)\left( n \right)-6\left( 2n \right)+4n=0\]
By simplifying the equation, we can write it as:
\[\Rightarrow 2{{n}^{2}}-8n=0\]
By taking 2n as common, we get the equation as:
\[\Rightarrow 2n\left( n-4 \right)=0\]
So, roots of the equation are: n = 0, n = 4.
As it is a polygon $n > 2.$ So, $n = 0$ is not possible.
Only possible root: $n = 4$ ----------- (10)
By substituting equation (10) in equation (6), we get:
\[\Rightarrow m=2n=2\left( 4 \right)=8\] ------- (11)
By equations (10), (11), we can say $(m, n) = (8, 4).$
Therefore, the number of sides of both polygons are 8, 4.

Note: Be careful while proving the angle of a polygon, don’t forget to consider the term sum of angles at O because the sum of all angles of triangles will include that angle. Also remember the condition why \[n\ne 0\], because by that you can substitute in the ratio. Whenever you have 2 variables, 2 equation systems it is always better and safer to use a substitution method.