Question

The angle between the legs of a compass is $ {{60}^{\circ }} $ and each leg is 10 cm long. How far apart are the points on which the legs of the compass rest?
(a) 5 cm
(b) 10 cm
(c) $ 5\sqrt{3} $ cm
(d) $ 10\sqrt{3} $ cm

Answer 1

Hint: Assume that the two legs of the compass rest on points A and B. Assume the joint part of the compass as point C. Now, a triangle ABC will be formed with two sides as 10 cm and the included angle as $ {{60}^{\circ }} $ . Use cosine rule given by: $ \operatorname{cosC}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} $ , to determine the value of ‘c’. In the above cosine formula: ‘C’ is the angle $ {{60}^{\circ }} $ , a and b are the sides opposite to the angles A and B, whose values are 10 cm. ‘c’ is the side opposite to angle ‘C’ whose value is to be determined.

Complete step-by-step answer:

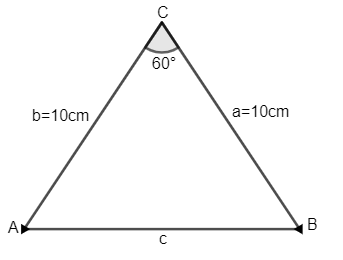
From the figure, we have assumed that the two legs of the compass rest on points A and B. The joint part of the compass is assumed to be point C.
Now, representing a, b and c as the sides opposite to that of the angles A, B and C, we have,
BC = a, AC = b and AB = c.
It is given that the angles between the legs of the compass is $ {{60}^{\circ }} $ . So, $ \angle C={{60}^{\circ }} $ .
Now, using cosine rule: $ \operatorname{cosC}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} $ , in the above triangle, we get,
 $ \cos {{60}^{\circ }}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} $
Substituting a = 10, b = 10 and $ \cos {{60}^{\circ }}=\dfrac{1}{2} $ , we get,
 $ \begin{align}
  & \dfrac{1}{2}=\dfrac{{{10}^{2}}+{{10}^{2}}-{{c}^{2}}}{2\times 10\times 10} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{100+100-{{c}^{2}}}{200} \\
 & \Rightarrow \dfrac{1}{2}=\dfrac{200-{{c}^{2}}}{200} \\
\end{align} $
By cross-multiplication we get,
 $ \begin{align}
  & 200-{{c}^{2}}=\dfrac{200}{2} \\
 & \Rightarrow 200-{{c}^{2}}=100 \\
 & \Rightarrow {{c}^{2}}=100 \\
\end{align} $
Taking square root both sides, we get,
c = 10 cm
Hence, option (b) is the correct answer.

Note: One may note that it is not necessary to use cosine rule or any formula to solve this question. We can directly come to the conclusion that c = 10 cm. we have been given that the two legs of the compass are of equal length, so it is concluded that the triangle is isosceles. Now, one angle is given as 60 degrees, so the other two equal angles of the isosceles triangle must be 60 degrees each, to satisfy the basic property of the triangle. Hence, each angle of the triangle is 60 degrees. Therefore, the final conclusion is that the triangle is equilateral. Hence, all the sides must be equal to 10 cm.