Question

The angle between hands of a clock when the time is 4.25 AM is: \[\]
A. $17{{\dfrac{1}{2}}^{\circ }}$\[\]
B. $14{{\dfrac{1}{2}}^{\circ }}$\[\]
C. $13{{\dfrac{1}{2}}^{\circ }}$\[\]
D. $12{{\dfrac{1}{2}}^{\circ }}$\[\]

Answer 1

Hint: We find the angle the minute hand makes when it moves from 12 to 5 as ${{\theta }_{M}}$. We find the angle hour hand makes when it moves from 12 o’clock to number 4, 5 as ${{\theta }_{4}},{{\theta }_{5}}$ respectively. We find the angle hour hand makes when it moves from 12 o’clock to 4.25AM as ${{\theta }_{H}}$ by weighted average. The required angle is ${{\theta }_{M}}-{{\theta }_{H}}$.\[\]

Complete step by step answer:
We know from rule of allegation that if there are two quantities are mixed at a ratio $a:b$($a,b$ are also called weights) and with amounts $A,B$ then their weighted average is
\[m=\dfrac{aA+bB}{a+B}\]
We know that when the minute hand or hour hand moves passing all the 12 numbers it subtends a complete angle of ${{360}^{\circ }}$. So the measure of the angle which the minute hand or hour hand makes passing from one number is
\[\theta =\dfrac{360}{12}={{30}^{\circ }}\]
We know that if the watch shows the time H:M where H is the hour and M is the minute passed hour then the hour hand will point towards somewhere between numbers H and H+1 at a ratio $M:60-M$.\[\]
We are asked the question to find the angle between the hands of a clock when the time is 4.25 AM. We know that at 4.25AM the minute hand will point towards the number 5 and hour hand will point somewhere between the number 4 and 5 at the ratio $25:\left( 60-25 \right)=25:35$. We have drawn the figure below. \[\]
 

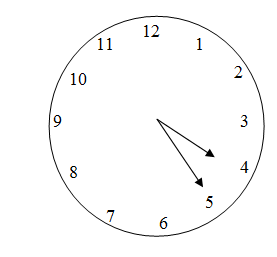
Let us denote the angle the minute hand makes when it from 12 o’clock to number 5 as ${{\theta }_{M}}$ and the angle hour hand makes when it moves from 12 o’clock to number 4, 5 and somewhere between 4 to 5 at ratio 25: 35 on 4.25AM as ${{\theta }_{4}},{{\theta }_{5}},{{\theta }_{H}}$ respectively. So the angle between hour hand and minute hand at the time 4.35 AM that is ${{\theta }_{HM}}={{\theta }_{M}}-{{\theta }_{H}}$\[\]

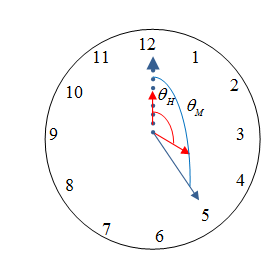
We observe that when the minute hand moves from 12 to 5 it passes 5 numbers. So we have,
\[{{\theta }_{M}}=5\times {{30}^{\circ }}={{150}^{\circ }}\]
We observe that when the hour hand moves from 12 to 4 it passes 4 numbers, when it passes 12 to 5 it passes 5 numbers. So we have,
\[\begin{align}
  & {{\theta }_{4}}=4\times {{30}^{\circ }}={{120}^{\circ }} \\
 & {{\theta }_{5}}=5\times {{30}^{\circ }}={{150}^{\circ }} \\
\end{align}\]
We can take weighted average of ${{\theta }_{4}},{{\theta }_{5}}$ with weights 35, 25 respectively to find the angle made by hour hand when it moves from 12 AM to 4.25 Am. So we have,
\[{{\theta }_{M}}=\dfrac{35\times {{\theta }_{4}}+25\times {{\theta }_{5}}}{25+35}=\dfrac{35\times 120+25\times 150}{25+35}=\dfrac{8250}{60}=132{{\dfrac{1}{2}}^{\circ }}\]
So the measure of required angle is
\[{{\theta }_{HM}}={{\theta }_{M}}-{{\theta }_{H}}=150-132\dfrac{1}{2}=17{{\dfrac{1}{2}}^{\circ }}\]

So, the correct answer is “Option A”.

Note: We note that we took the weights for ${{\theta }_{4}},{{\theta }_{5}}$ as 35, 25 not 25, 35 as obtained from the ratio 25:35 because we are measuring the angle difference from the minute hand not the hour hand. We can directly find the required angle as by the formula $\Delta \theta =\left| {{\theta }_{h}}-{{\theta }_{m}} \right|$ where ${{\theta }_{h}}={{0.5}^{\circ }}\left( 60\times H\times M \right)$ and ${{\theta }_{m}}={{6}^{\circ }}\times M$ where ${{\theta }_{h}},{{\theta }_{m}}$ are the angle of our hand and minute hand measured clockwise from 12 o’clock positions, $H$ is the hour and $M$ is the minute passed hour.