Question

The acute angle between two straight lines passing through the point M(-6,-8) and the points in which the line segment 2x + y + 10 = 0 enclosed between the coordinate axes is divided in the ratio 1 : 2 : 2 in the direction from the point of its interaction with the x-axis to the point of intersection with the y-axis is
(A) \[\dfrac{\pi }{3}\]
(B) \[\dfrac{\pi }{4}\]
(C) \[\dfrac{\pi }{6}\]
(D) \[\dfrac{\pi }{12}\]

Answer 1

Hint: Find the coordinates of point B and C by using the formula of point of division as B divides the line AD in ratio 1:4 internally and C divides the line AD in the ratio 3:2 internally. Then find the slopes \[{{m}_{1}}\] and \[{{m}_{2}}\] of the lines CM and BM respectively using the formula \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\] where \[{{x}_{1}}\], \[{{x}_{2}}\], \[{{y}_{1}}\], \[{{y}_{2}}\] are the coordinates of respective points. Find the angle \[\theta \] made by the slopes \[{{m}_{1}}\] and \[{{m}_{2}}\] using the formula \[\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\] to get the final answer.

Complete step-by-step answer:
Given that the straight line passes through the point M (-6,-8). The line segment 2x + y + 10 = 0 enclosed between the coordinate axes is divided in the ratio 1 : 2 : 2.

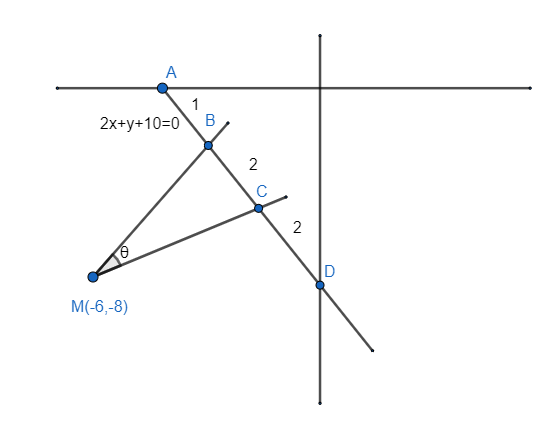
First we have to find the coordinates of B and C. 
The coordinates of A and D are given by the line intercept form.
Line intercept form is \[\dfrac{x}{a}+\dfrac{y}{b}=1\]
The line intercept form for the line 2x + y + 10 = 0 is \[\dfrac{x}{-5}+\dfrac{y}{-10}=1\]
The coordinates of A and D are (-5,0) and (0,-10) respectively.
Formula: Any point P which divides the line segment joining the points A \[\left( {{x}_{1}},{{y}_{1}} \right)\], B \[\left( {{x}_{2}},{{y}_{2}} \right)\]in the ratio m:n internally is given by 
\[P=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
Similarly B divides AD in the ratio 1 : 4 internally. From the above formula we get point B as,
\[B=\left[ \dfrac{1\left( 0 \right)+4\left( -5 \right)}{1+4},\dfrac{1\left( -10 \right)+4\left( 0 \right)}{1+4} \right]\]
\[B=\left( -4,-2 \right)\]
Similarly C divides AD in the ratio 3 : 2 internally. From the above formula we get point C as,
\[C=\left[ \dfrac{3\left( 0 \right)+2\left( -5 \right)}{3+2},\dfrac{3\left( -10 \right)+2\left( 0 \right)}{3+2} \right]\]
\[C=\left( -2,-6 \right)\]

For line CM the coordinates are \[\left( -2,-6 \right)\] and \[\left( -6,-8 \right)\].
Slope of line CM is \[{{m}_{1}}=\dfrac{-8+2}{-6+4}=3\]

For line BM the coordinates are \[\left( -4,-2 \right)\] and \[\left( -6,-8 \right)\].
Slope of line BM is \[{{m}_{2}}=\dfrac{-8+6}{-6+2}=\dfrac{1}{2}\]
The formula for finding the angle from slopes is \[\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\]
\[\begin{align}
  & \tan \theta =\dfrac{3-\dfrac{1}{2}}{1+\dfrac{3}{2}} \\
 & \tan \theta =1
\end{align}\]
That means \[\theta =\dfrac{\pi }{4}\]

So, the correct answer is “Option B”.

Note: As the formulas play a key role in this problem they should be handy. As there are 4 points on the same line and the points divide the line in different ratios, be careful in writing all those. From the slopes angle is calculated using the formula of \[\tan \theta \].