Question

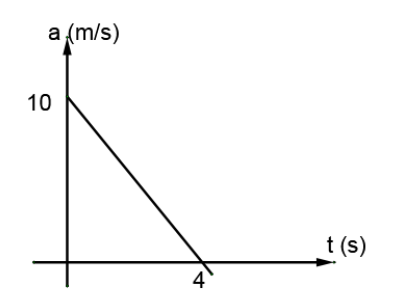
The acceleration time graph of a particle moving along a straight line is as shown in Fig. At what time the particle acquires its initial velocity?

Answer 1

Hint: We are given an acceleration- time graph, as it is a straight line we can use it to find acceleration as a function of time. Then use this equation to get a relation between velocity and time, which will easily lead us to answer.
Formula used: if $\left( {{y_1},{x_1}} \right)$ & $\left( {{y_2},{x_2}} \right)$ are points on a straight line, then its equation in two point form can be given by:
$y = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)(x - {x_1}) + {y_1}$
The formula for acceleration is
$a = \dfrac{{dv}}{{dt}}$ … (1)

COMPLETE STEP BY STEP SOLUTION:
Here in the acceleration-time graph the two points given to us are (4, 0) & (0, 10). If we represent acceleration by a and time by t and the we can get the equation of the line by applying the two point form in the following way:
\[\begin{array}{l}
\left( {{x_1},{y_1}} \right) = \left( {4,0} \right)\\
\left( {{x_2},{y_2}} \right) = \left( {0,10} \right)
\end{array}\]

$\begin{array}{l}
y = \left( {\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}} \right)(x - {x_1}) + {y_1}\\
y = \left( {\dfrac{{10 - 0}}{{0 - 4}}} \right)(x - 4) + 0\\
y = - \dfrac{5}{2}(x - 4)
\end{array}$
Now we know that x = t and y = a, so we can write that
$\begin{array}{l}
a = - \dfrac{5}{2}\left( {t - 4} \right)\\
\therefore a = - \dfrac{5}{2}t + 10
\end{array}$
Now, we know that acceleration is equal to the time derivative of velocity, therefore we can write using equation 1,
$\dfrac{{dv}}{{dt}} = - \dfrac{5}{2}t + 10$
$dv = \left( { - \dfrac{5}{2}t + 10} \right)dt$
Let us assume initial velocity c, integrating both used using limit
\[\int\limits_c^v {dv} = \int\limits_0^t {\left( { - \dfrac{5}{2}t + 10} \right)dt} \]
On solving we get
$v = - \dfrac{5}{4}{t^2} + 10t + c$
Where v is velocity at any time t
For same initial velocity
$v = c$
$\begin{array}{l}
 - \dfrac{5}{4}{t^2} + 10t + c = c\\
 \Rightarrow \dfrac{5}{4}{t^2} - 10t = 0\\
 \Rightarrow 5{t^2} - 40t = 0\\
 \Rightarrow 5t\left( {t - 8} \right) = 0\\
\therefore t = 0,8
\end{array}$

Therefore the particle acquires its initial velocity at t = 0s and t = 8s.

Note: Alternative approach for this question can be
The area of acceleration-time graphs give change in velocity and according to the question change in velocity from t=0 s to the required time must be zero. Thus the area under the graph must be zero. And the area under the graph is found by integration. So we can integrate the acceleration-time function till time t when the answer becomes zero. And it will be our required time.
\[\int\limits_0^t {\left( { - \dfrac{5}{2}t + 10} \right)dt} = 0\]
On solving t=8 s.