Question

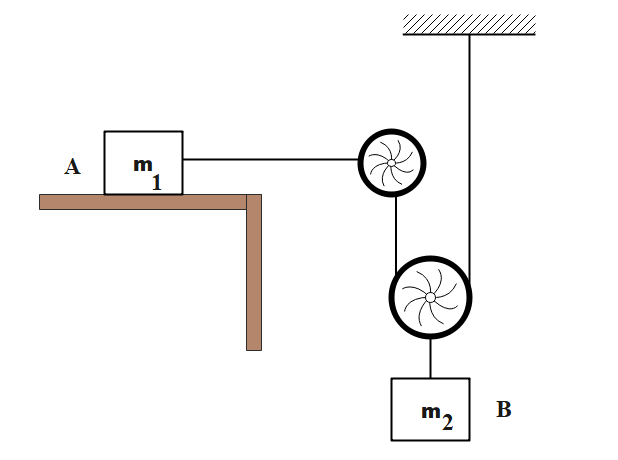
The acceleration of the block B in the figure will be:

A. $\dfrac{{{m_2}g}}{{\left( {4{m_1} + {m_2}} \right)}}$
B. $\dfrac{{2{m_1}g}}{{\left( {{m_1} + 4{m_2}} \right)}}$
C. $\dfrac{{2{m_2}g}}{{\left( {4{m_1} + {m_2}} \right)}}$
D. $\dfrac{{2{m_1}g}}{{\left( {{m_1} + {m_2}} \right)}}$

Answer 1

Hint: Tension is defined as the drawing force acting on a body when it is hung from objects such as string, cable, chain, etc. It is represented by the letter ‘T’. Tension is a force that’s why it's unit is expressed in Newtons (N). So, to find the solution of the given question we will use the concept of tension.
Formula Used: $T = W \pm ma$
Where ‘W’ is the weight of the body, ‘a’ is the acceleration of the moving body and ‘m’ is the mass of the body.

Complete answer:
Let us first draw a free body diagram of the given two blocks ‘A’ and ‘B’ for a better understanding of the question,

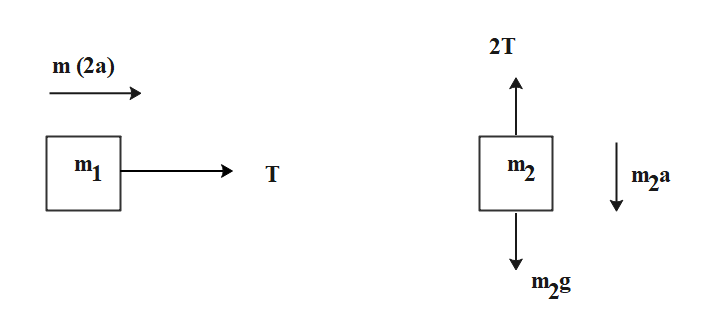
Now, from the given figure we can see that when the block ‘${m_2}$’ moves downward with an acceleration ‘a’. Now, the acceleration of mass ‘m’ would be ‘2a’, since it covers double distance at the same time in comparison to the mass of the block ‘${m_2}$’.
Let us assume that ‘T’ is the tension which is acting through the string,
From the free body diagram of block ‘A’ and ‘B’ that we drew earlier we get that,
T = ${m_1}2a$ --(1)
${m_2}g - 2T = {m_2}a$ --(2)
From the equation (1) and equation (2) we get,
$\therefore a = \dfrac{{{m_2}g}}{{\left( {4{m_1} + {m_2}} \right)}}$

Hence, option (A) is the correct answer.

Note:
As we know, every physical object which is in contact with any other object exerts some force on it. These contact forces are determined by the names based on the types of objects. When one of the forces exerting an object is a string, cable or chain, we call it tension.
The tension force is known as the force which gets transmitted through a cable, string or wire when pulled by the forces working from the opposite sides. The tension force is directed over the length of the wire and pulls energy equally on the bodies at the ends.