Question

The \[ABCD\] is a square with each side \[12\,\,cm\]. \[P\] is a point on \[BC\] such that the area of \[\vartriangle ABP\] : area of trapezium \[APCD = 1:5\]. Find the length of \[CP\].

Answer 1

Hint:Here in this question, we have to find the length of the side CP in a square \[ABCD\] by using the ratio of area of \[\vartriangle ABP\] : area of trapezium \[APCD\]. For this the take the unknown length as \[x\] and by using the formula of area of triangle \[ = \dfrac{1}{2} \times base \times height\] and area of trapezium \[ = \dfrac{1}{2}\left( {a + b} \right) \times height\], where ‘\[a\]’ and ‘\[b\]’ are the bases of trapezium and by further simplification we get the required solution.

Complete step by step answer:
Consider the question: Given, a square \[ABCD\] with each side \[12\,\,cm\] and \[P\] is a point on side \[BC\], Join the points \[AP\] it gives a triangle \[\vartriangle ABP\] and trapezium \[APCD\].
Given the ratio: \[\dfrac{\text{Area of triangle}\,\vartriangle ABP}{\text{Area of trapezium APCD}} = \dfrac{1}{5}\]

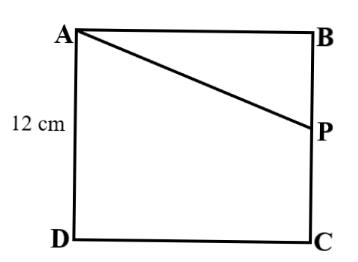
In a square \[ABCD\].
\[AB = BC = CD = AD = 12\,cm\]
Let us consider, the length of \[CP = x\]
The length of \[BP = BC - CP\]
\[\therefore \,\,\,BP = 12 - x\]
Consider the formula of area of triangle \[ = \dfrac{1}{2} \times base \times height\]
In \[\vartriangle ABP\]
\[ \Rightarrow \text{Area of}\,\vartriangle ABP = \dfrac{1}{2} \times AB \times BP\]
On substituting the values, we have
\[ \Rightarrow \,\,\dfrac{1}{2} \times 12 \times \left( {12 - x} \right)\]

On simplification, we get
\[\therefore \text{Area of}\,\vartriangle ABP = 6\left( {12 - x} \right)\] ------(1)
Consider the formula of area of trapezium\[ = \dfrac{1}{2}\left( {a + b} \right) \times height\]
 Where, ‘\[a\]’ and ‘\[b\]’ are the bases of trapezium
In trapezium \[ABCD\]
\[ \Rightarrow \text{Area of trapezium APCD} = \dfrac{1}{2} \times \left( {AD + CP} \right) \times DC\]
On substituting the values, we have
\[ \Rightarrow \text{Area of trapezium APCD} = \dfrac{1}{2} \times \left( {12 + x} \right) \times 12\]
On simplification, we get
\[\therefore \text{Area of trapezium APCD} = 6\left( {12 + x} \right)\] -----(2)

Now, consider the given ratio
\[ \Rightarrow \,\,\,\dfrac{\text{Area of triangle}\,\vartriangle ABP}{\text{Area of trapezium APCD}} = \dfrac{1}{5}\]
By the equation (1) and (2), we have
\[ \Rightarrow \,\,\,\dfrac{{6\left( {12 - x} \right)}}{{6\left( {12 + x} \right)}} = \dfrac{1}{5}\]
\[ \Rightarrow \,\,\,\dfrac{{12 - x}}{{12 + x}} = \dfrac{1}{5}\]
On cross multiplication, we have
\[ \Rightarrow \,\,\,5\left( {12 - x} \right) = 12 + x\]
\[ \Rightarrow \,\,\,60 - 5x = 12 + x\]
Take all the variable \[x\] terms to the LHS, then on rearranging
\[ \Rightarrow \,\,\,x + 5x = 60 - 12\]
\[ \Rightarrow \,\,\,6x = 48\]
Divide both side by 6
\[ \Rightarrow \,\,\,x = \dfrac{{48}}{6}\]
\[\therefore \,\,\,x = 8\,\,cm\]

Therefore, the length of \[CP = 8\,\,cm\].

Note:Diagram representation for this type of questions is very important to make understanding and solving easier and a ratio is obtained by division. We can express it as a fraction, the convention is that the first mentioned item is a numerator and the second is a denominator. Remember the suitable formula like area of triangle, area of trapezium etc.