Question

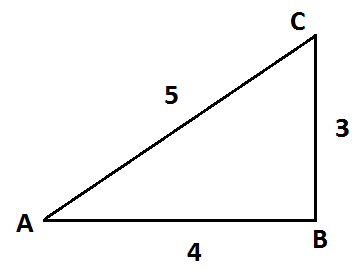
The $ ABC $ is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. $ {I_{AB}},{I_{BC}},{I_{CA}} $ are the moments of inertia of the plate about $ AB,BC $ and $ CA $ respectively. Then which of the following conditions/conditions will satisfy?

(A) $ {I_{AB}} + {I_{BC}} = {I_{CA}} $
(B) $ {I_{CA}} $ is maximum
(C) $ {I_{AB}} > {I_{BC}} $
(D) $ {I_{BC}} > {I_{AB}} $

Answer 1

Hint :Find the moment of Inertia of the triangle about its different base and compare them.
Use the formula, the Moment of Inertia of a triangular plate about its base is, $ {I_B} = \dfrac{{M{h^2}}}{6} $ ,Where $ M $ is the total mass of the triangular plate and $ h $ is the height about it’s any of the sides.


Complete Step By Step Answer:
We know that the Moment of Inertia of a triangular plate about its base is, $ {I_B} = \dfrac{{M{h^2}}}{6} $ , Where $ M $ is the total mass of the triangular plate and $ h $ is the height about its any of the sides.
Here, we have a right -angle triangle, so we can find the height taking each of the sides as base easily.
Now, let’s first take $ AB $ as the base of the triangle. So, then the height of the triangle becomes $ BC $
Therefore, Moment of Inertia about $ AB $ will be, $ {I_{AB}} = \dfrac{{M{h_1}^2}}{6} $
Here, $ {h_1} = 3 $
 $ \therefore $ $ {I_{AB}} = \dfrac{{M \cdot {3^2}}}{6} = \dfrac{{9M}}{6} $
Now, let’s take $ BC $ as the base of the triangle. So, then the height of the triangle becomes $ AB $
Therefore, Moment of Inertia about $ BC $ will be , $ {I_{BC}} = \dfrac{{M{h_2}^2}}{6} $
Here, $ {h_2} = 4 $
 $ \therefore $ $ {I_{BC}} = \dfrac{{M \cdot {4^2}}}{6} = \dfrac{{16M}}{6} $
Now, take $ CA $ as the base of the triangle. Then, Moment of Inertia about $ CA $ will be $ {I_{CA}} = \dfrac{{M{h_3}^2}}{6} $
Here, we have to calculate $ {h_3} $ . Now, from the figure we can find $ \sin \theta $ for $ \Delta ABC $ and also for triangle $ \Delta BCD $ . So, for $ \Delta ABC $ , $ \sin \theta = \dfrac{{perp.}}{{hyp.}} = \dfrac{{AB}}{{AC}} $

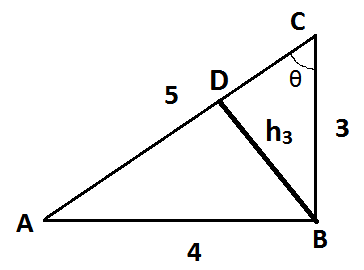
 $ \therefore $ $ \sin \theta = \dfrac{4}{5} $
So, for $ \Delta BCD $ , $ \sin \theta = \dfrac{{BD}}{{BC}} $
 $ \therefore $ $ \sin \theta = \dfrac{{{h_3}}}{3} $
So, we can equate both the $ \sin \theta $
Hence, equating we get, $ {h_3} = \dfrac{{3 \cdot 4}}{5} $
Therefore, $ {h_3} = \dfrac{{12}}{5} $
Hence, $ {I_{CA}} = \dfrac{{M{h_3}^2}}{6} = \dfrac{{M{{(\dfrac{{12}}{5})}^2}}}{6} = \dfrac{{144}}{5} \cdot \dfrac{M}{6} $
That becomes,
 $ {I_{CA}} = \dfrac{{28.8M}}{6} $
Therefore we have, $ {I_{AB}} = \dfrac{{9M}}{6} $ , $ {I_{BC}} = \dfrac{{16M}}{6} $ and $ {I_{CA}} = \dfrac{{28.8M}}{6} $
Hence, $ {I_{AB}} = \dfrac{{9M}}{6} < {I_{BC}} = \dfrac{{16M}}{6} < {I_{CA}} = \dfrac{{28.8M}}{6} $
Now, we can see that $ {I_{BC}} > {I_{AB}} $ and we can also see that the sum of $ {I_{AB}} $ and $ {I_{BC}} $ is, $ {I_{AB}} + {I_{BC}} = \dfrac{{9M}}{6} + \dfrac{{16M}}{6} = \dfrac{{25M}}{6} \ne {I_{CA}} $
Therefore, Option (D ) is correct only.

Note :
 $ \bullet $ Calculating Moment of Inertia is a very lengthy calculation to do, so, it is advised to memorize the Moment of Inertia for different geometrical shapes for convenience.
 $ \bullet $ This problem can also be solved using parallel axes theorem .If we can find the distance between the centre of mass and the sides then we can compare the moment of inertia easily.