
The ${6563A^\circ}$ line emitted by a hydrogen atom in a star is found to be red shifted by ${5A^\circ}$. The speed with which the star is receding from the earth is
(A) $17.3 \times {10^3}m/s$
(B) $4.29 \times {10^7}m/s$
(C) $3.39 \times {10^5}m/s$
(D) $2.29 \times {10^5}m/s$
Answer
585.6k+ views
Hint: Doppler shift is the change in frequency of a wave in relation to an observer who is moving relation to the wave source. Hence, wavelength is changed or shifted
Complete step by step answer:
When a body that is emitting radiation has a non-zero radial velocity relative to an observer the wavelength of the emission will be shortened or lengthened, depending upon whether the body is moving towards or away from an observer.
This change in wavelength or frequency is known as the Doppler shift.
The formula of Doppler shift for wavelength is given as
$\dfrac{{\Delta \lambda }}{\lambda } = \dfrac{V}{C}$
Where
$\Delta \lambda = $ Wavelength shift
$\lambda = $ Initial value length
$C = $ Speed of light in vacuum
In question, it is given that
$\Delta \lambda ={5A^\circ}= 5 \times {10^{ - 10}}m$
$\lambda = {6563A^\circ} = 6563 \times {10^{ - 10}}m$
$C = 3 \times {10^8}m/s$
$V = ?$
So, $V = C \times \dfrac{{\Delta \lambda }}{\lambda }$
$V = 3 \times {10^8} \times \dfrac{{5 \times {{10}^{ - 10}}}}{{6563 \times {{10}^{ - 10}}}}$
$V = \dfrac{{15 \times {{10}^8}}}{{6563}}$
$V = 0.0022855 \times {10^8}$
$V \simeq 2.29 \times {10^5}m/s$
So, the correct answer is “Option D”.
Note:
In many problems of Doppler effect, they asked for frequency change which is given as
1.
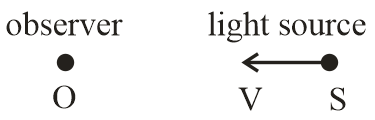
Frequency $f' = \left( {1 + \dfrac{V}{C}} \right)f$
Wavelength $\lambda ' = \left( {1 - \dfrac{V}{C}} \right)\lambda $
(Blue shift)
2.
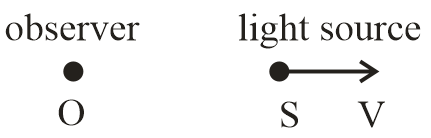
Frequency $f' = \left( {1 - \dfrac{V}{C}} \right)f$
Wavelength $\lambda ' = \left( {1 + \dfrac{V}{C}} \right)\lambda $
(Red shift)
Complete step by step answer:
When a body that is emitting radiation has a non-zero radial velocity relative to an observer the wavelength of the emission will be shortened or lengthened, depending upon whether the body is moving towards or away from an observer.
This change in wavelength or frequency is known as the Doppler shift.
The formula of Doppler shift for wavelength is given as
$\dfrac{{\Delta \lambda }}{\lambda } = \dfrac{V}{C}$
Where
$\Delta \lambda = $ Wavelength shift
$\lambda = $ Initial value length
$C = $ Speed of light in vacuum
In question, it is given that
$\Delta \lambda ={5A^\circ}= 5 \times {10^{ - 10}}m$
$\lambda = {6563A^\circ} = 6563 \times {10^{ - 10}}m$
$C = 3 \times {10^8}m/s$
$V = ?$
So, $V = C \times \dfrac{{\Delta \lambda }}{\lambda }$
$V = 3 \times {10^8} \times \dfrac{{5 \times {{10}^{ - 10}}}}{{6563 \times {{10}^{ - 10}}}}$
$V = \dfrac{{15 \times {{10}^8}}}{{6563}}$
$V = 0.0022855 \times {10^8}$
$V \simeq 2.29 \times {10^5}m/s$
So, the correct answer is “Option D”.
Note:
In many problems of Doppler effect, they asked for frequency change which is given as
1.
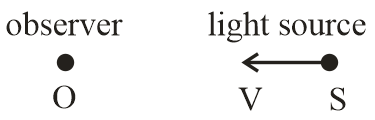
Frequency $f' = \left( {1 + \dfrac{V}{C}} \right)f$
Wavelength $\lambda ' = \left( {1 - \dfrac{V}{C}} \right)\lambda $
(Blue shift)
2.
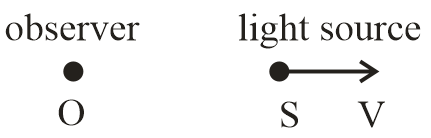
Frequency $f' = \left( {1 - \dfrac{V}{C}} \right)f$
Wavelength $\lambda ' = \left( {1 + \dfrac{V}{C}} \right)\lambda $
(Red shift)
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




