Question

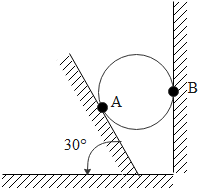
The 50 kg homogeneous smooth sphere rests on the ${30^ \circ }$ incline A and bears against the smooth vertical wall B. The contact force at B is ($g = 10\dfrac{m}{{{s^2}}}$)

\[\begin{array}{l}
A.\;\;\;\;\;\;\;\;250N\\
B.\;\;\;\;\;\;\;\;0N\\
C.\;\;\;\;\;\;\;\dfrac{{\;500}}{{\sqrt 3 }}N\\
D.\;\;\;\;\;\;\;\;250N
\end{array}\]

Answer 1

Hint: In order to solve this problem, first we need to draw a free body diagram which will show us the various forces acting on the system. Then comparing the directions of various forces, we can obtain the equations of motion for the system. By solving these equations, we may obtain the contact force.

Complete step by step solution:
Let us first draw a free body diagram of the ball which involves two normal forces at A & B. These forces are perpendicular to walls from which they are applied and also to the gravitational force. Their magnitude is given to be equal to $50 \times 10 = 500N$ (where the gravitational force is equal to the product of the mass of the ball and the acceleration due to gravity.)
Let us call the normal from wall A to be ${N_A}$ and the normal from wall B to be ${N_B}$. Now by doing some simple calculations, we can find out the angle between the vertical and ${N_A}$ which is equal to the angle made by incline & floor which is equal to ${30^ \circ }$

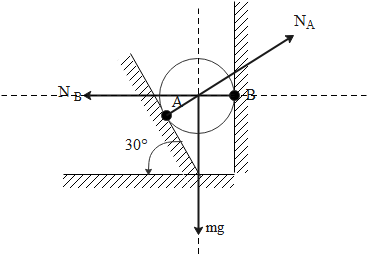
Now, we can resolve ${N_A}$ into its horizontal & vertical components which are given to be ${N_A}\cos {30^ \circ }$ & ${N_A}\sin {30^ \circ }$ which is equal to $\dfrac{{\sqrt 3 {N_A}}}{2}$ & $\dfrac{{{N_A}}}{2}$ respectively.
Since the sphere is in equilibrium forces along vertical & horizontal should be balanced. On equating them we get
$mg = {N_A}\cos {30^ \circ }$
$\dfrac{{\sqrt 3 {N_A}}}{2} = 500$ … (1)
${N_B} = {N_A}\sin {30^ \circ }$
${N_B} = \dfrac{{{N_A}}}{2}$ … (2)
Putting value of ${N_A}$ from equation 1
${N_B} = \dfrac{{2 \times 500}}{{\sqrt 3 \times 2}} = \dfrac{{500}}{{\sqrt 3 }}$ N
Hence the correct option is C.

Note: Students often make mistakes while taking angle between components of force. The angle should be calculated carefully. Also, it must be remembered that normal always acts perpendicular to surface and point of contact. Hence in the case of a sphere it always passes from the center.