Question

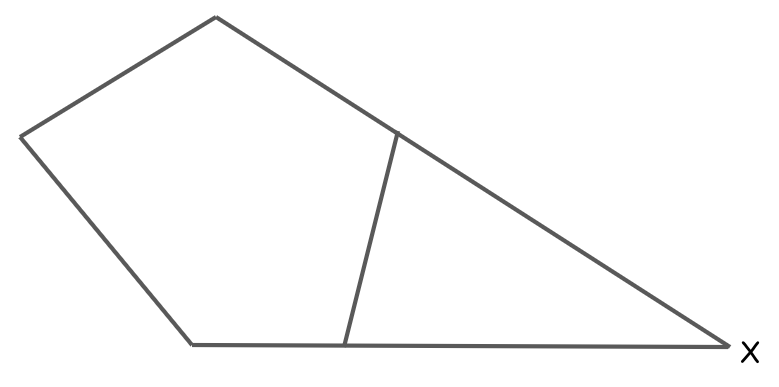
The 2 nonadjacent sides of a regular pentagon (5 congruent and 5 congruent interior angles) are extended to meet at point \[X\] as shown in the above figure. Find the measure of \[\angle X\].

A.\[18^\circ \]
B.\[30^\circ \]
C.\[36^\circ \]
D.\[45^\circ \]
E.\[72^\circ \]

Answer 1

Hint: First, we will use that the sum of interior angles of the pentagon is \[\left( {n - 2} \right) \times 180^\circ \], where \[n\] is the number of sides. Then take \[n = 5\] in this formula and then in a regular pentagon, the value of each of the interior angle is computed by dividing the above value of 5

Complete step-by-step answer:
We are given that the 2 non adjacent sides of a regular pentagon (5 congruent and 5 congruent interior angles) are extended to meet at point \[X\].
We know that the sum of interior angles of the pentagon is \[\left( {n - 2} \right) \times 180^\circ \], where \[n\] is the number of sides.

Since we know that the sides of the given figure are \[n = 5\].
Substituting the value of \[n\] in the above formula of sum of interior angles of the pentagon, we get
\[
   \Rightarrow \left( {5 - 2} \right) \times 180^\circ \\
   \Rightarrow 3 \times 180^\circ \\
   \Rightarrow 540^\circ \\
 \]
Since we are given that a regular pentagon, the value of each of the interior angle is computed by dividing the above value of 5, we get
\[
   \Rightarrow \dfrac{{540^\circ }}{5} \\
   \Rightarrow 108^\circ \\
 \]
We know that the two base angles of the triangle form a linear pair with the interior angles of the pentagon.
So, we will the measure of the two base angle of the triangle by subtracting \[180^\circ \] by \[108^\circ \], we get
\[
   \Rightarrow 180^\circ - 108^\circ \\
   \Rightarrow 72^\circ \\
 \]
Thus we have from the above figure that
\[
   \Rightarrow 180^\circ - \left( {72^\circ + 72^\circ } \right) \\
   \Rightarrow 180^\circ - 144^\circ \\
   \Rightarrow 36^\circ \\
 \]

Hence, option C is correct.

Note: In solving this question, we have multiplied the given ratio with some unknown variable. Then use the fact that the sum of angle of the triangle is \[180^\circ \left( {n - 2} \right)\], where \[n\] is the number of sides to obtain a linear equation.