Question

The 120N force is applied as shown to one end of the curved wrench. If \[\alpha = 30^\circ \], calculate the moment of \[F\] about the center O of the belt. Determine the value of \[\alpha \] which would maximize the moment about O, state the value of this maximum moment.

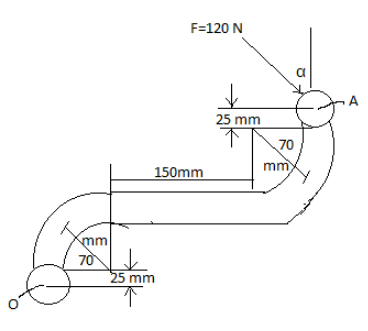
Answer 1

Hint: Use the equation for the moment of force in terms of the force and the perpendicular distance between point of action of force and the point about which the moment of force is to be determined. Use the horizontal and vertical components of force to calculate the final moment of force. Use the condition for the maximum moment of force and again determine the required angle and moment of force.

Formula used:
The moment of the force is given by
\[\tau = F{r_ \bot }\] …… (1)
Here, \[\tau \] is the moment of force, \[F\] is the force and \[{r_ \bot }\] is the perpendicular distance between the point of action of the force and the centre of the circular arc around which moment of force vector is acting.
The angle \[\alpha \] between the components of the moment of force and moment of force \[\tau \] is given by
\[\alpha = {\tan ^{ - 1}}\left( {\dfrac{{{\tau _y}}}{{{\tau _x}}}} \right)\] …… (2)
Here, \[{\tau _x}\] and \[{\tau _y}\] are the horizontal and vertical components of the moment of force.

Complete step by step answer:
The given diagram in terms of components of force is as follows:

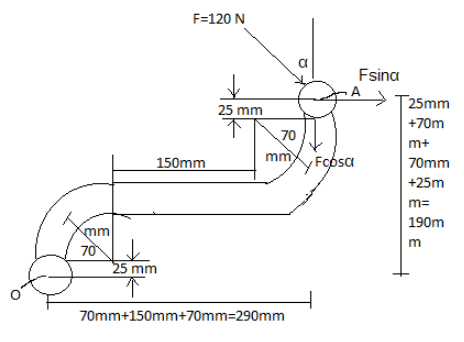
In the problem, it is given that the force \[F = 120\,{\text{N}}\] is acting to one end of the wrench.We can see that in figure, the force has two components \[F\sin \alpha \] and \[F\cos \alpha \] in horizontal and vertical directions respectively.Let us calculate the perpendicular distance \[{r_h}\] between the horizontal force \[F\sin \alpha \] and the point O.
\[{r_h} = \left( {25\,{\text{mm}}} \right) + \left( {70\,{\text{mm}}} \right) + \left( {70\,{\text{mm}}} \right) + \left( {25\,{\text{mm}}} \right)\]
\[ \Rightarrow {r_h} = 190\,{\text{mm}}\]
The perpendicular distance between the horizontal force \[F\sin \alpha \] and the point O is \[190\,{\text{mm}}\].
Let us calculate the perpendicular distance \[{r_v}\] between the vertical force \[F\cos \alpha \] and the point O.
\[{r_v} = \left( {70\,{\text{mm}}} \right) + \left( {150\,{\text{mm}}} \right) + \left( {70\,{\text{mm}}} \right)\]
\[ \Rightarrow {r_v} = 290\,{\text{mm}}\]
The perpendicular distance between the vertical force \[F\cos \alpha \] and the point O is \[290\,{\text{mm}}\].
Now we can determine the moment of force by adding the moment of horizontal and vertical components of force.
\[\tau = F\sin \alpha {r_h} + F\cos \alpha {r_v}\]
Substitute \[120\,{\text{N}}\] for \[F\], \[30^\circ \] for \[\alpha \], \[190\,{\text{mm}}\] for \[{r_h}\] and \[290\,{\text{mm}}\] for \[{r_v}\] in the above equation.
\[\tau = \left( {120\,{\text{N}}} \right)\sin 30^\circ \left( {190\,{\text{mm}}} \right) + \left( {120\,{\text{N}}} \right)\cos 30^\circ \left( {290\,{\text{mm}}} \right)\]
\[ \Rightarrow \tau = 41500\,{\text{N}} \cdot {\text{mm}}\]
\[ \Rightarrow \tau = 41.5\,{\text{N}} \cdot {\text{m}}\]
Hence, the moment of force about the center of the belt is \[41.5\,{\text{N}} \cdot {\text{m}}\].
The value of the moment of force will be maximum only when the force is perpendicular to OA (the line joining point of action A and center of belt O).
Let us now determine the angle \[\alpha \] for which moment of force will be maximum.
Substitute \[\left( {120\,{\text{N}}} \right)\left( {190\,{\text{mm}}} \right)\] for \[{\tau _y}\] and \[\left( {120\,{\text{N}}} \right)\left( {290\,{\text{mm}}} \right)\] for \[{\tau _x}\] in equation (2).
\[\alpha = {\tan ^{ - 1}}\left( {\dfrac{{\left( {120\,{\text{N}}} \right)\left( {190\,{\text{mm}}} \right)}}{{\left( {120\,{\text{N}}} \right)\left( {290\,{\text{mm}}} \right)}}} \right)\]
\[ \Rightarrow \alpha = {\tan ^{ - 1}}\left( {\dfrac{{190}}{{290}}} \right)\]
\[ \Rightarrow \alpha = 33.2^\circ \]
The value of maximum moment of inertia \[{\tau _{\max }}\] for the determined value of angle \[\alpha \].
\[{\tau _{\max }} = F\sqrt {r_h^2 + r_v^2} \]
Substitute \[120\,{\text{N}}\] for \[F\], \[190\,{\text{mm}}\] for \[{r_h}\] and \[290\,{\text{mm}}\] for \[{r_v}\] in the above equation.
\[{\tau _{\max }} = \left( {120\,{\text{N}}} \right)\sqrt {{{\left( {190\,{\text{mm}}} \right)}^2} + {{\left( {290\,{\text{mm}}} \right)}^2}} \]
\[ \Rightarrow {\tau _{\max }} = 41603.85\,{\text{N}} \cdot {\text{mm}}\]
\[ \therefore {\tau _{\max }} = 41.6\,{\text{N}} \cdot {\text{m}}\]

Hence, the maximum moment of force is \[41.6\,{\text{N}} \cdot {\text{m}}\] for the angle \[33.2^\circ \].

Note: One can also determine the angle for which the moment of force on the system is maximum by taking the derivative of the moment of force \[\tau \] with respect to angle \[\alpha \] and equating it to zero. Also, the students may forget to convert the unit of the final moment of force in the SI system of units as the distances in the diagram are given in millimeters.