Question

The 105,000 kg space shuttle is doing a training exercise in outer space. How much energy would it take to bump up the space shuttle from an altitude of 500 km to 1000 km above the surface of the earth?

Assume the radius of the earth is $6.37 \times {10^6}$m and the mass of the Earth is $5.98 \times {10^{24}}$kg.
$\left( A \right) 2.07 \times {10^{11}}J$
$\left( B \right) 2.10 \times {10^{13}}J$
$\left( C \right) 4.15 \times {10^{11}}J$
$\left( D \right) - 4.19 \times {10^{13}}J$
$\left( E \right) - 2.09 \times {10^{13}}J$

Answer 1

Hint: We will first read the question properly and we will write down the given information. Then by using the given information we will make a diagram. We will use the formula, i.e., $E = \dfrac{{G{M_1}{M_2}}}{2}\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]$ , we will get the required answer.

Formula used - $E = \dfrac{{G{M_1}{M_2}}}{2}\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]$

Complete step-by-step answer:

Here in the question, it is given that a space shuttle whose mass is 105,000 kg is doing a training exercise in outer space and we have to find out the energy required to bump up the space shuttle from an altitude of 500 km to 1000 km above the surface of the earth.

Given that,

Mass of the space shuttle$\left( {{M_s}} \right)$ = 150,000 kg
Mass of the Earth $\left( {{M_e}} \right)$ = $5.98 \times {10^{24}}$kg
Radius of the Earth $\left( {{R_e}} \right)$ = $6.37 \times {10^6}$m

From the radius of the Earth we can also find out the radius of the orbits, therefore
Radius of initial orbit $\left( {{r_1}} \right)$ = $\left( {6.37 + 0.5} \right) \times {10^6}$= $6.87 \times {10^6}m$
Radius of final orbit $\left( {{r_2}} \right)$ = $\left( {6.37 + 1.0} \right) \times {10^6} = 7.37 \times {10^6}m$

With the help of this we can make a diagram which is as follows:

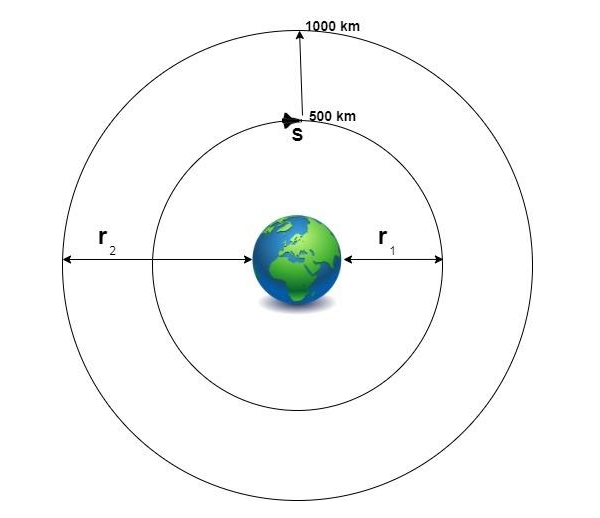
Now, we have to find the energy required to bump up the space shuttle from the initial orbit to the final orbit, therefore,

Energy required $\left( E \right) = \dfrac{{G{M_e}{M_s}}}{2}\left[ {\dfrac{1}{{{r_1}}} - \dfrac{1}{{{r_2}}}} \right]$

We have all the values except of G but we know that G stands for the universal gravitational constant and which is equal to
$6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$ .
$\therefore E = \dfrac{{6.67 \times {{10}^{ - 11}} \times 5.98 \times {{10}^{24}} \times 105000}}{2}\left[ {\dfrac{1}{{6.87 \times {{10}^6}}} - \dfrac{1}{{7.37 \times {{10}^6}}}} \right]$

After calculation process, we obtain,

$E = 2.07 \times {10^{11}}J$

Hence, option A is the right answer.

Note: Universal gravitational constant may be defined as the force of attraction between two bodies of unit mass each and placed unit distance apart. In SI, it is equal to the force of attraction between two bodies of 1kg each and placed 1m apart and its value in SI system is
$6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.