Question

The 10 students of batch B feel they have some conceptual doubt on circular-permutation. Mr. Mathew called them into the discussion room and asked them to sit down around a circular table which is surrounded by 13 chairs. Mr. Mathew told that his adjacent seat should not remain empty. Then find the number of ways in which the students can sit around a round table if Mr. Mathew also sits on a chair.

Answer 1

Hint: First, before proceeding for this, we must draw the diagram of the condition where on a circular table with 13 chairs let M be the fixed chair of Mr. Mathew and A and B are the adjacent chairs of Mr. Mathew which has to be filled. Then, for the selection of two students to be seated at A and B positions from the total of 10 students with both changing their seat is given by ${}^{10}{{C}_{2}}\times 2$. Then, for the arrangement of the anything within something is always defined by permutation which gives the final result.

Complete step by step answer:
In this question, we are supposed to find the number of ways in which the students can sit around a round table if Mr. Mathew also sits on a chair where 10 students are to be seated in a way so that adjacent chair of Mr. Mathew would not be empty from the 13 total chairs in the room.
So, before proceeding for this, we must draw the diagram of the condition where on a circular table with 13 chairs let M be the fixed chair of Mr. Mathew and A and B are the adjacent chairs of Mr. Mathew which has to be filled as:

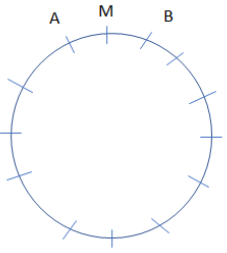
Now, for the selection of two students be seated at A and B positions from the total of 10 students is given by:
${}^{10}{{C}_{2}}$
Moreover, we can see that A and B seated students can also interchange their positions, so we get the total arrangement of students adjacent to Mr. Mathew as:
${}^{10}{{C}_{2}}\times 2$
Now, we are left with 10 seats and 8 students and we have to arrange 8 students in 10 seats.
So, for the arrangement of anything within something is always defined by permutation.
Then, for the arrangement of 8 students in 10 seats left is given by:
${}^{10}{{P}_{8}}$
So, now the total number of the ways in which number of ways, in which the students can sit around a round table if Mr. Mathew also sit on a chair where 10 students are to be seated in a way so that adjacent chair of Mr. Mathew would not be empty from the 13 total chairs in room is given by:
${}^{10}{{C}_{2}}\times 2\times {}^{10}{{P}_{8}}$

Hence, the required answer is ${}^{10}{{C}_{2}}\times 2\times {}^{10}{{P}_{8}}$.

Note:
Now, to solve these types of questions we need to know some of the basics of the permutation and combination. So, the formula for the combination which is used for selection is given by
$^{n}{{C}_{r}}=\dfrac{n!}{\left( n-r \right)!r!}$
Also, the formula for the permutation which is used for arrangement is given by:
$^{n}{{P}_{r}}=\dfrac{n!}{\left( n-r \right)!}$