Question

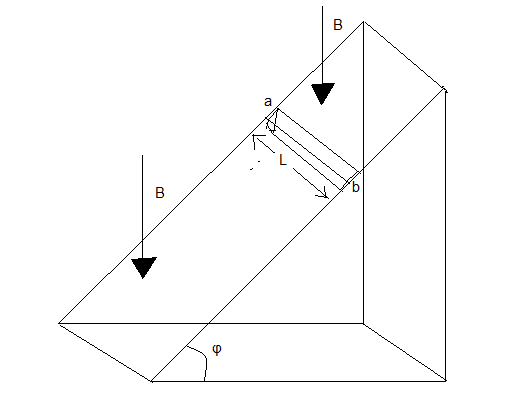
What is the terminal speed of the bar?

 $ \left( A \right)\dfrac{{mgR}}{{{B^2}{l^2}\sin \phi }} \\
\left( B \right)\dfrac{{mgR\cos \phi }}{{{B^2}{l^2}{{\sin }^2}\phi }} \\
\left( C \right)\dfrac{{mgR\sin \phi }}{{{B^2}{l^2}{{\cos }^2}\phi }} \\
\left( D \right)\dfrac{{mgR\sin \phi }}{{{B^2}{l^2}\cos \phi }} \\ $

Answer 1

Hint :In order to solve the question, we are going to equate the magnetic field with the gravitational force, as in this condition only the bar will attain a terminal velocity. The terminal velocity is then derived from the equation by simplifying it and further solving the equation.
The formula used here is
Gravitational force is given by $ mg\sin \phi $
And magnetic force is given by $ Ilb\cos \phi $
Here, $ mg\sin \phi = Ilb\cos \phi $
Here $ m $ is the mass of the bar, $ g $ is the acceleration of gravity, $ B $ is the magnetic force, $ l $ is the length of the rod, $ b $ is the breadth, $ \phi $ is the angle.
The current in the bar $ I $ is given as
 $ I = \dfrac{{Blv\cos \phi }}{R} $

Complete Step By Step Answer:
The bar attains the terminal velocity when the magnetic field is balanced by the gravitational force, so if we equate the two forces then, the equation becomes
 $ mg\sin \phi = Ilb\cos \phi $
Here $ m $ is the mass of the bar, $ g $ is the acceleration of gravity, $ B $ is the magnetic force, $ l $ is the length of the rod, $ b $ is the breadth, $ \phi $ is the angle.
Where on left hand side, we have the gravitational force and on the right hand side, we have the magnetic field
The current in the bar $ I $ is given as
 $ I = \dfrac{{Blv\cos \phi }}{R} $
Using this relation in the above equation
 $ mg\sin \phi = \dfrac{{{B^2}{l^2}v{{\cos }^2}\phi }}{R} $
Rearranging the terms we get, the relation for velocity
 $ v = \dfrac{{mgR\sin \phi }}{{{B^2}{l^2}{{\cos }^2}\phi }} $
Hence, the terminal speed of the bar $ v = \dfrac{{mgR\sin \phi }}{{{B^2}{l^2}{{\cos }^2}\phi }} $
Hence, option $ \left( C \right)\dfrac{{mg\sin \phi R}}{{{B^2}{l^2}{{\cos }^2}\phi }} $ is correct.

Note :
Terminal velocity is the steady speed that is achieved by the freely falling objects under gravity in air or in some medium. In this question, it is a very important step to see what all forces are acting on the bar and then checking the condition of equilibrium where the terminal velocity can be attained.