Question

Teja and Murali on either side of a temple of 30 meters height, observe its top at the angles of elevation ${{30}^{\circ }}$ and ${{60}^{\circ }}$ respectively. Find the distance between the two boys.

Answer 1

Hint: We will apply the formula of trigonometric ratios. We consider one angle which is less than 90 degrees and take that angle as a guide. Then we will apply trigonometric ratios like $\sin \left( \theta \right)=\dfrac{\text{perpendicular}}{\text{Hypotenuse}}\,\,,\,\,\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$ and $\tan \left( \theta \right)=\dfrac{\text{perpendicular}}{\text{Base}}$.

Complete step-by-step solution -
The diagram for the question is given below.

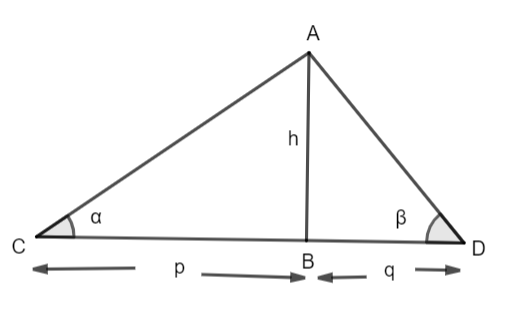
We are clearly given the height of the temple which is 30 metres. We need to find the base which is actually the distance between C and D. The distance is shown in the diagram as CD. Let us suppose here that Murali is standing on point D. This is because the point D represents angle $\beta $ which is ${{60}^{\circ }}$ and Teja is standing on the point C. This point C represents the angle ${{30}^{\circ }}$. We will suppose that the AB is the height of the temple which is 30 meters. And we are measuring the distance of Teja standing at point C from point B. Also we will measure the distance of Murali from point B to D where he is standing. For that we consider CB as p meters and BD as q meters.
The diagram is now illustrated as shown below.

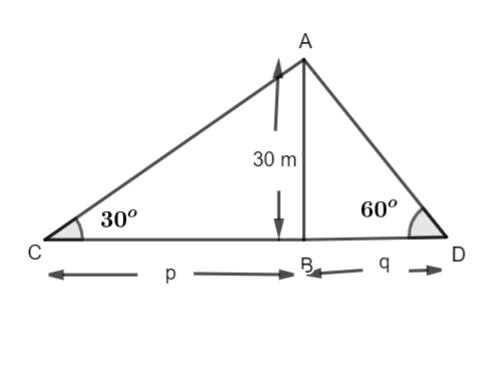
We will solve this question with the help of trigonometric ratios. But here we need to select as to which trigonometric operation will solve this question. For that we will watch the figure again. In the diagram we are given just the height and the base is considered by us. Therefore we will select that trigonometric operation which includes height and the base. So clearly we need tan operator here. Now, for measuring distance CB we have
$\begin{align}
  & \tan \left( \alpha \right)=\dfrac{\text{perpendicular}}{\text{base}} \\
 & \Rightarrow \tan \left( \alpha \right)=\dfrac{h}{p} \\
 & \Rightarrow \tan \left( \alpha \right)=\dfrac{h}{p} \\
 & \Rightarrow \tan \left( \alpha \right)=\dfrac{30}{p} \\
\end{align}$
We have the angle $\alpha ={{30}^{\circ }}$.
$\begin{align}
  & \Rightarrow \tan \left( {{30}^{\circ }} \right)=\dfrac{30}{p} \\
 & \Rightarrow p=\dfrac{30}{\tan \left( {{30}^{\circ }} \right)} \\
\end{align}$
As the value of $\tan \left( {{30}^{\circ }} \right)$ is $\dfrac{1}{\sqrt{3}}$.
$\begin{align}
  & \Rightarrow p=\dfrac{30}{\tan \left( {{30}^{\circ }} \right)} \\
 & \Rightarrow p=\dfrac{30}{\dfrac{1}{\sqrt{3}}} \\
 & \Rightarrow p=\dfrac{30}{1}\times \dfrac{\sqrt{3}}{1} \\
 & \Rightarrow p=30\sqrt{3} \\
\end{align}$
Now, we will for measuring distance BD we have
$\begin{align}
  & \tan \left( \beta \right)=\dfrac{\text{perpendicular}}{\text{base}} \\
 & \Rightarrow \tan \left( \beta \right)=\dfrac{h}{q} \\
 & \Rightarrow \tan \left( \beta \right)=\dfrac{h}{q} \\
 & \Rightarrow \tan \left( \beta \right)=\dfrac{30}{q} \\
\end{align}$
We have the angle $\beta ={{60}^{\circ }}$. Therefore, we have
$\begin{align}
  & \Rightarrow \tan \left( {{60}^{\circ }} \right)=\dfrac{30}{q} \\
 & \Rightarrow q=\dfrac{30}{\tan \left( {{60}^{\circ }} \right)} \\
\end{align}$
As the value of $\tan \left( {{60}^{\circ }} \right)$ is $\sqrt{3}$.
$\begin{align}
  & \Rightarrow q=\dfrac{30}{\tan \left( {{60}^{\circ }} \right)} \\
 & \Rightarrow q=\dfrac{30}{\sqrt{3}} \\
 & \Rightarrow q=\dfrac{30}{1}\times \dfrac{1}{\sqrt{3}} \\
 & \Rightarrow q=\dfrac{30}{\sqrt{3}} \\
\end{align}$
After rationalizing we have,
$\begin{align}
  & \Rightarrow q=\dfrac{30\sqrt{3}}{3} \\
 & \Rightarrow q=10\sqrt{3} \\
\end{align}$
Therefore, the distance between C and D is given by the sum of p + q. That is $10\sqrt{3}+30\sqrt{3}$ which is $40\sqrt{3}$.

Note: We could also have selected sine or cosine operations but only if we had given the values of the two hypotenuses given in the figure. The distance can never be negative. If by chance the distance is coming as a negative value then one needs to check the mistake.