Question

Tangents to a circle at points P and Q intersect at point R. if $PQ=6$ and $PR=5$ then, the radius of the circle is:
a) $\dfrac{13}{3}$
b) $4$
c) $\dfrac{15}{4}$
d) $\dfrac{16}{5}$

Answer 1

Hint: In this given question, in order to get the solution, we must first show that PQ is divided into two halves by the line segment RO where O is the center of the referred circle by R-H-S congruence criterion. Then, we can get the magnitude of length of RM where M is the intersection point of RO and PQ using Pythagoras theorem. Thereafter, we can show $\Delta PMR$ similar to $\Delta OPR$ by R-H-S similarity criterion and use the obtained and given measurements of lengths to get the required radius of the circle.

Complete step-by-step answer:

In this question, we are given that tangents to a circle at points P and Q intersect at point R, $PQ=6$ and $PR=5$. We are asked to find out the measurement of the radius of the circle. With the given information, we make the following figure:

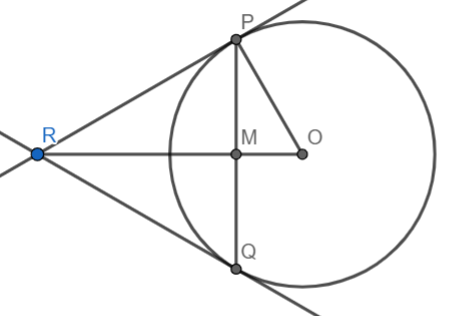
In this figure, RP and RQ are tangents to the circle with center O. PQ is the line segment joining the intersection points of the tangents and the circle and M is the intersection point of RO and PQ.

In this solution, we are going to use the R-H-S congruence criterion which states that,

If in two right angle triangles the hypotenuses and either of the sides other than the hypotenuses are equal, then the two triangles are congruent with all corresponding parts equal.

Also, we are going to use the A-A similarity criterion which states that,
If in two triangles if two angles are equal in both the triangles, then the two triangles are similar with all corresponding parts proportional with the same ratio.

We, will also use the Pythagoras Theorem which states that,

In a right angle triangle, the sum of squares of the two sides other than the hypotenuse is equal to the square of the hypotenuse.

The process of solving is as follows:

In $\Delta PRM$ and $\Delta QRM$,

$\begin{align}

  & RM=RM\left( common \right) \\

 & RP=RQ\left( \text{tangents from the external point to a circle are equal} \right) \\

 & \angle PMR=\angle QMR\left( each\text{ }{{90}^{\circ }} \right) \\

 & \Rightarrow \Delta PRM\cong \Delta QRM\left( by\text{ R-H-S conruency criterion} \right)
\\

 & \Rightarrow PM=QM\left( CPCT \right)...........(1.1) \\

\end{align}$

Now,

\[\begin{align}

  & PQ=6 \\

 & \Rightarrow PM+QM=6 \\

 & \Rightarrow 2PM=6\left( as\text{ }PM=QM;1.1 \right) \\

 & \Rightarrow PM=3=QM..........(1.2) \\

\end{align}\]

In $\Delta PMR$, as $\angle M$ is a right angle, by using Pythagoras theorem, we get,

$\begin{align}

  & P{{R}^{2}}=P{{M}^{2}}+M{{R}^{2}} \\

 & \Rightarrow M{{R}^{2}}=P{{R}^{2}}-P{{M}^{2}} \\

 & \Rightarrow M{{R}^{2}}={{5}^{2}}-{{3}^{2}} \\

 & \Rightarrow MR=4..........(1.3) \\

\end{align}$

Now, in $\Delta PMR$ and $\Delta OPR$,

\[\begin{align}

  & \angle M=\angle P\left( each\text{ }{{90}^{\circ }} \right) \\

 & \angle PRM=\angle ORP\left( common \right) \\

 & \Rightarrow \Delta PMR\sim \Delta OPR\left( by\text{ }A-A\text{ similarity criterion} \right) \\

 & \Rightarrow \dfrac{PM}{OP}=\dfrac{MR}{PR}..........(1.4) \\

\end{align}\]

Now, putting all obtained values from 1.1, 1.2 and 1.3 in 1.4, we get

\[\begin{align}

  & \dfrac{PM}{OP}=\dfrac{MR}{PR} \\

 & \Rightarrow \dfrac{3}{OP}=\dfrac{4}{5} \\

 & \Rightarrow OP=\dfrac{15}{4}..........(1.5) \\

\end{align}\]

Hence, we have obtained the value of radius OP, that is equal to $\dfrac{15}{4}$.

Therefore, the correct option to this given question is option (c) $\dfrac{15}{4}$.

Note: Here, we could have also used algebra in place of geometry to solve this question. We could have taken an unknown length as a variable x and could have solved this given question and still would have arrived at the same answer as it would have been only another approach towards the question to solve it and get the required answer.