Question

How many tangents can be drawn on a circle from a point?

Answer 1

Hint: For solving this problem, first we need to specify the location of the point whether it is outside of the circle, on the circle or inside of the circle. By critically analysing at each point we can easily identify the number of tangents formed.

Complete step-by-step answer:
A tangent is a line that touches the circle at exactly one point. Now, for our problem we have the following cases:
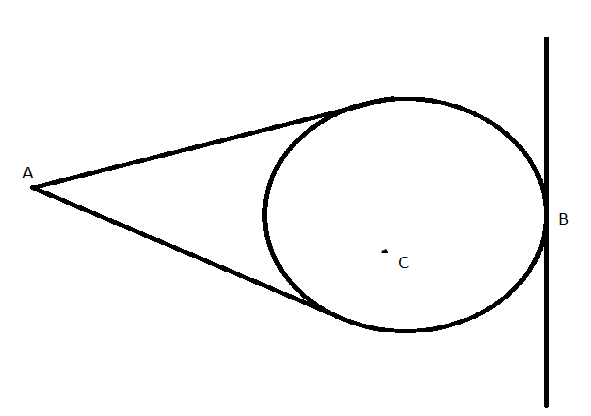
If the point lies outside the circle, then two tangents can be drawn to a circle from a point as there exists two lines extending from the point that will touch the circle.
If the point lies on the circle, then it has one and only one tangent. A tangent line has to be perpendicular to the radius of the circle at this point. Since, perpendicular lines through a given point are unique, therefore only one tangent could be formed.
If a point is inside the circle, then no tangent line can be drawn through a point, since any such line must be a secant line. It will look like a chord inside a circle.

Note: The key concepts involved in solving this problem is the knowledge of geometrical figures particularly tangent to a circle. It is solved by using visualisation above but this problem can also be solved alternatively by using diagrams.