Question

How many tangents can be drawn from a point outside the circle?
$
  {\text{A}}{\text{. 1}} \\
  {\text{B}}{\text{. 2}} \\
  {\text{C}}{\text{. 3}} \\
  {\text{D}}{\text{. 0}} \\
 $

Answer 1

Hint: Here, we will proceed by visualizing exactly how many tangents (straight lines that touch the circle at only one point) to a circle can be drawn from any point outside the circle with the help of a figure.

Complete step-by-step answer:

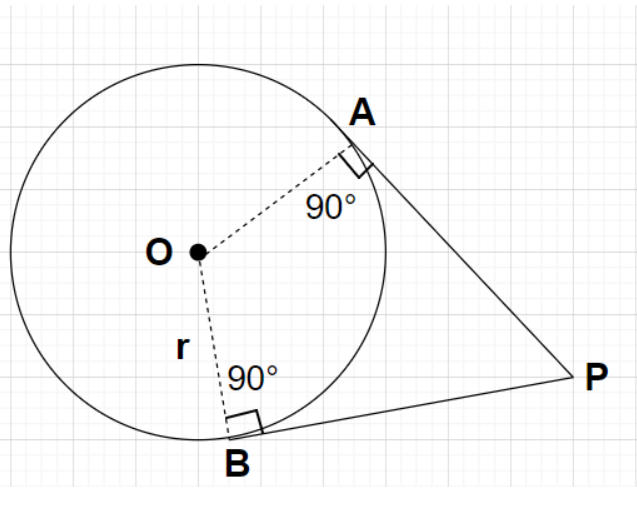
Tangents to any circle are the lines which touch the circle at only one point and don't intersect that circle. The angle between the tangents to any circle and the radius line of that circle are always right angles (i.e., equal to ${90^\circ}$).
Let us consider a circle having centre at point O and having radius equal to r. Taking any point P outside the circle. Here, OA and OB are the radius lines. Clearly, we can see that only two lines can be drawn through this point P in such a way that these lines touch the circle at only one point and these lines are the required tangents to the circle through an outside point. Here, AP and BP are the tangents to the drawn circle of radius r from a point P outside the circle.
Therefore, two (2) tangents can be drawn from a point outside the circle.
Hence, option B is correct.

Note: It is also important that no tangent line can be drawn to any circle through a point which lies inside the circle because that line which only cuts the circle at two points will become the secant line. In the figure, we can also see that the tangents AP and BP are perpendicular to the radius lines OA and OB respectively at the point of tangency.