Question

Tangents are drawn from the point \[P\left( 1,-1 \right)\] to the circle \[{{x}^{2}}+{{y}^{2}}-4x-6y-3=0\] with center C. A and B are the points of contact. The area of the triangle formed by a pair of tangents and the corresponding chord of contact is
(A) \[\dfrac{8}{17}\]
(B) \[\dfrac{4}{17}\]
(C) \[\dfrac{6}{17}\]
(D) none of these

Answer 1

Hint: It is given that the equation of the circle is \[{{x}^{2}}+{{y}^{2}}-4x-6y-3=0\] . We know the standard equation of the circle \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] . Now, equation \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] and \[{{x}^{2}}+{{y}^{2}}-4x-6y-3=0\] , and get the value of g, f, and c. Now, get the coordinate of the center \[\left( -g,-f \right)\] and then, calculate the radius of the circle, \[\sqrt{{{g}^{2}}+{{f}^{2}}-c}\] . Using the distance formula, \[\text{distance}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\] , calculate the distance CP. Now, in \[\Delta CAP\] calculate the cosine of \[\angle APC\] . In \[\Delta AOP\] , we have \[\cos \angle APO=\dfrac{Base}{Hypotenuse}=\dfrac{OP}{PA}=\dfrac{OP}{\sqrt{17}}\] . Now, using the value of the cosine of \[\angle APC\] , calculate the value of the side OP. We know the Pythagoras theorem, \[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] . Now, apply the Pythagoras theorem for \[\Delta AOP\] and get the value of OA. We know the area of the triangle, \[Area=\dfrac{1}{2}\times \left( perpendicular \right)\times \left( base \right)\] . Now, use this formula and calculate the area of \[\Delta AOP\] . We also know the property that the line joining the center and the point from where a pair of tangents are drawn to the circle divides the triangle formed by a pair of tangents and the corresponding chord of contact into triangles of equal area. Using this property we can say that, Area of \[\Delta AOP\] = Area of \[\Delta BOP\] . We also have, Area of \[\Delta ABP\] = Area of \[\Delta AOP\] + Area of \[\Delta BOP\] . Now, solve it further and get the value of the area of \[\Delta ABP\] .

Complete step-by-step answer:
According to the question, it is given that
The equation of the circle = \[{{x}^{2}}+{{y}^{2}}-4x-6y-3=0\] …………………………………….(1)
The coordinate of P point from where a pair of tangents have been drawn on the circle =
\[\left( 1,-1 \right)\] ………………………………………….(2)
We know the standard equation of the circle, \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0\] …………………………………..(3)
The center of the circle = \[\left( -g,-f \right)\] …………………………………..(4)
The radius of the circle = \[\sqrt{{{g}^{2}}+{{f}^{2}}-c}\] ………………………………………..(5)
Now, on comparing equation (1) and equation (3), we get
\[g=-2\] ……………………………………(6)
\[f=-3\] …………………………………...(7)
\[c=-3\] ……………………………………..(8)
It is given that C is the center of the circle.
From equation (4), equation (6), and equation (7), we have
The center C of the given circle =\[\left( 2,3 \right)\] ………………………………….(9)
From equation (5), equation (6), equation (7), and equation (8), we get
The radius of the circle = \[\sqrt{{{\left( -2 \right)}^{2}}+{{\left( -3 \right)}^{2}}-\left( -3 \right)}=\sqrt{16}=4\] ………………………………………..(10)

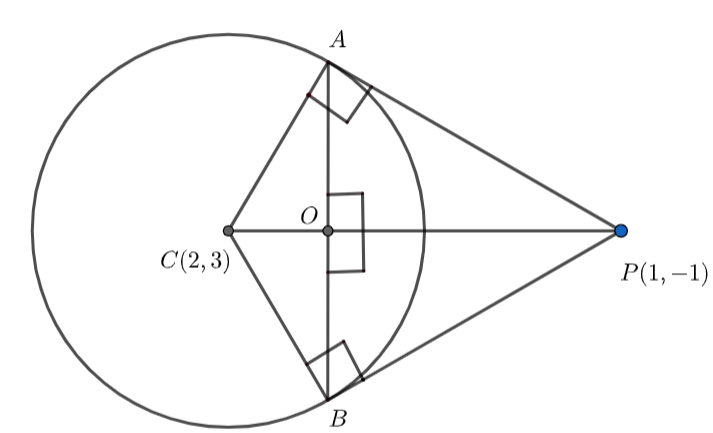
It is given that tangents are drawn from the point P to the circle at point A and point B.
Using this property we can say that radius CA and CB are perpendicular to the tangents PA and PB.
From equation (2) and equation (9), we have the coordinates of point P and point C.
The coordinate of point P = \[\left( 1,-1 \right)\] ……………………………….(11)
The coordinate of point C = \[\left( 2,3 \right)\] …………………………………….(12)
Now, using the distance formula, \[\text{distance}=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}\] …………………………………(13)
Now, from equation (11), equation (12), and equation (13), we get
\[\begin{align}
  & \Rightarrow CP=\sqrt{{{\left( 2-1 \right)}^{2}}+{{\left( 3-\left( -1 \right) \right)}^{2}}} \\
 & \Rightarrow CP=\sqrt{{{1}^{2}}+{{4}^{2}}} \\
\end{align}\]
\[\Rightarrow CP=\sqrt{17}\] …………………………………(14)
We know the Pythagoras theorem, \[{{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\] ………………………………..(15)
Since \[\Delta CAP\] is a right-angled triangle so, we can use the Pythagoras theorem here.
In \[\Delta CAP\] we have,
Perpendicular = AC = radius = 4 (equation (10)) ………………………………………(16)
Hypotenuse = CP = \[\sqrt{17}\] (equation (14))
Base = PA
\[\angle CAP=90{}^\circ \] (CA is perpendicular to the tangent PA)
Now, using the Pythagoras theorem,
\[\begin{align}
  & \Rightarrow {{\left( CP \right)}^{2}}={{\left( CA \right)}^{2}}+{{\left( PA \right)}^{2}} \\
 & \Rightarrow {{\left( \sqrt{17} \right)}^{2}}={{\left( 4 \right)}^{2}}+{{\left( PA \right)}^{2}} \\
 & \Rightarrow 17-16={{\left( PA \right)}^{2}} \\
 & \Rightarrow 1={{\left( PA \right)}^{2}} \\
\end{align}\]
\[\Rightarrow 1=PA\] ………………………………………..(17)
Now, In \[\Delta CAP\] we have,
Perpendicular = AC = radius = 4 (equation (10)) ………………………………………(18)
Hypotenuse = CP = \[\sqrt{17}\] (equation (14))
Base = PA = 1 (equation (17))
\[\cos \angle APC=\dfrac{Base}{Hypotenuse}=\dfrac{PA}{CP}=\dfrac{1}{\sqrt{17}}\] …………………………………………..(19)
We know the property that the line the center and the point from where a pair of tangents are drawn to the circle is perpendicular to the chord of contact.
Using this property we can say that CP is perpendicular to the chord of contact AB.
Now, in \[\Delta AOP\] , we have
\[\angle APC=\angle APO\] (from the figure) ……………………………………..(20)
PA = 1 (equation (17))
\[\cos \angle APO=\dfrac{Base}{Hypotenuse}=\dfrac{OP}{PA}=\dfrac{OP}{\sqrt{17}}\] …………………………………………(21)
Now, from equation (19), equation (20), and equation (21), we get
\[\Rightarrow \dfrac{OP}{1}=\dfrac{1}{\sqrt{17}}\]
\[\Rightarrow OP=\dfrac{1}{\sqrt{17}}\] ……………………………………….(22)
Using the Pythagoras theorem for \[\Delta AOP\] , we get
\[\Rightarrow {{\left( Hypotenuse \right)}^{2}}={{\left( Perpendicular \right)}^{2}}+{{\left( Base \right)}^{2}}\]
\[\Rightarrow {{\left( PA \right)}^{2}}={{\left( OA \right)}^{2}}+{{\left( OP \right)}^{2}}\] …………………………………………(23)
Now, from equation (17), equation (22), and equation (23), we get
\[\begin{align}
  & \Rightarrow {{\left( 1 \right)}^{2}}={{\left( OA \right)}^{2}}+{{\left( \dfrac{1}{\sqrt{17}} \right)}^{2}} \\
 & \Rightarrow 1-\dfrac{1}{17}={{\left( OA \right)}^{2}} \\
 & \Rightarrow \dfrac{16}{17}={{\left( OA \right)}^{2}} \\
\end{align}\]
\[\Rightarrow \dfrac{4}{\sqrt{17}}=OA\] ………………………………………….(24)
Here, in \[\Delta AOP\] , we have
Perpendicular = OA = \[\dfrac{4}{\sqrt{17}}\] ………………………………………….(25)
Base = OP = \[\dfrac{1}{\sqrt{17}}\] …………………………………………….(26)
We know the formula for the area of the triangle, \[Area=\dfrac{1}{2}\times \left( perpendicular \right)\times \left( base \right)\] …………………………………………(27)
Now, from equation (25), equation (26), and equation (27), we get
Area of \[\Delta AOP\] = \[\dfrac{1}{2}\times \left( \dfrac{4}{\sqrt{17}} \right)\times \left( \dfrac{1}{\sqrt{17}} \right)\] …………………………………………….(28)
We also know the property that the line joining the center and the point from where a pair of tangents are drawn to the circle divides the triangle formed by a pair of tangents and the corresponding chord of contact into triangles of equal area.
Using this property we can say that,
Area of \[\Delta AOP\] = Area of \[\Delta BOP\] ……………………………………(29)
Now, from equation (28) and equation (29), we get
Area of \[\Delta AOP\] = Area of \[\Delta BOP\] = \[\dfrac{1}{2}\times \dfrac{4}{17}\] ………………………………….(30)
From the figure, we can say that
Area of \[\Delta ABP\] = Area of \[\Delta AOP\] + Area of \[\Delta BOP\] …………………………………………..(31)
Now, from equation (30) and equation (31), we get
Area of \[\Delta ABP\] = \[\dfrac{1}{2}\times \dfrac{4}{17}+\dfrac{1}{2}\times \dfrac{4}{17}=\dfrac{1}{2}\times \dfrac{8}{17}=\dfrac{4}{17}\] sq units.
Therefore, the area of \[\Delta ABP\] is equal to \[\dfrac{4}{17}\] sq units .

So, the correct answer is “Option B”.

Note: In this question, one might get confused in the property that the line joining the center and the point from where a pair of tangents are drawn to the circle divides the triangle formed by a pair of tangents and the corresponding chord of contact into triangles of equal area.
We can remove this confusion by proving it.

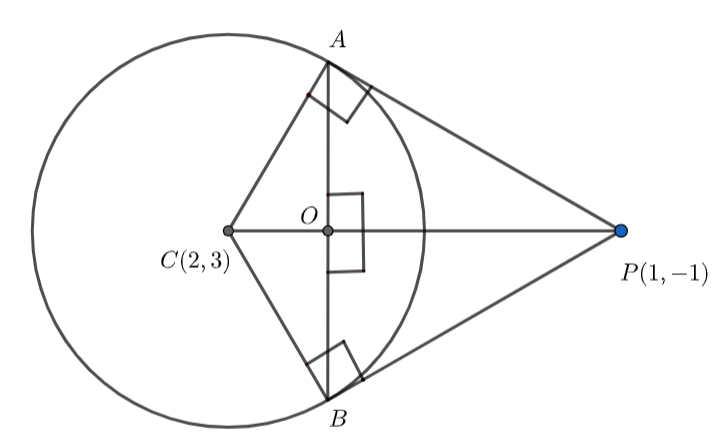
In \[\Delta AOP\] and \[\Delta BOP\] , we have
\[\angle AOP=\angle BOP=90{}^\circ \]
PA = PB (lengths of the tangents drawn from an external point are always equal)
OP = OP (common sides)
So, \[\Delta AOP\cong \Delta BOP\] (Right Hypotenuse side)
We know that the area of the congruent triangles is always equal.
Therefore, Area of \[\Delta AOP\] = Area of \[\Delta BOP\] .