Question

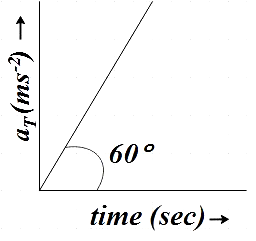
Tangential acceleration of a particle moving in a circle of radius 1m varies with time t as (initial velocity of particle is zero). Time after which total acceleration of particle makes an angle of $30{}^\circ $ with the radial acceleration is

Answer 1

Hint: Express the given graph in the form of the standard expression for a straight line graph. Put that in the expression of tangential acceleration as the derivative of velocity and thus find velocity of motion. Now you could find the tangential acceleration from the same. Now the vector sum of these two accelerations will give you the magnitude total acceleration (a), after which you could express ${{a}_{T}}$ as the component of a and hence get the answer.
Formula used:
Expression for centripetal acceleration,
${{a}_{C}}=\dfrac{{{v}^{2}}}{r}$

Complete answer:
We see that the given graph is a straight line and we know that a straight line graph is given by,
$y=mx+c$ ……………………. (1)
Where m is the slope of the given graph and c is the y intercept
We know that slope m is given by,
$m=\tan \theta $
Where $\theta $ is the angle at which the graph is inclined, so, here$\theta =60{}^\circ $
Slope, $m=\tan 60{}^\circ $
Also, the y intercept c = 0 here.
So (1) becomes,
${{a}_{T}}=\tan 60{}^\circ t+0$
$\Rightarrow {{a}_{T}}=\sqrt{3}t$ ………………………….. (2)
We know that tangential acceleration or the instantaneous acceleration is given by,
${{a}_{T}}=\dfrac{dv}{dt}=\sqrt{3}t$
$\Rightarrow dv=\sqrt{3}tdt$
Integrating on both sides,
$\int{dv=\int{\sqrt{3}}}tdt$
$\Rightarrow v=\dfrac{\sqrt{3}{{t}^{2}}}{2}$
Since the body is undergoing circular motion, there is centripetal or the radial acceleration acting on it, which is given by,
${{a}_{C}}=\dfrac{{{v}^{2}}}{r}=\dfrac{{{\left( \dfrac{\sqrt{3}}{2}{{t}^{2}} \right)}^{2}}}{r}$
But r=1m,
$\Rightarrow {{a}_{C}}=\dfrac{3}{4}{{t}^{4}}$
For total acceleration of particle making an angle of$30{}^\circ $ with the radial acceleration,

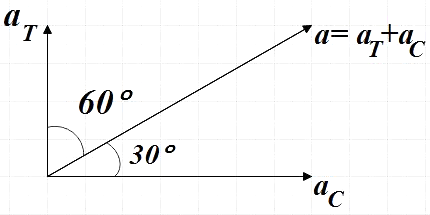
The total acceleration is given by the vector sum of ${{a}_{T}}$ and ${{a}_{C}}$ at$90{}^\circ $
$a=\sqrt{{{a}_{T}}^{2}+{{a}_{C}}^{2}+2{{a}_{T}}{{a}_{C}}\cos 90}$
$\Rightarrow a=\sqrt{{{\left( \sqrt{3}t \right)}^{2}}+{{\left( \dfrac{3}{4}{{t}^{4}} \right)}^{2}}}$
$\Rightarrow a=\sqrt{3{{t}^{2}}+\dfrac{9}{16}{{t}^{8}}}$
Tangential acceleration when expressed as a component of a is given by,
${{a}_{T}}=a\cos \theta $
$\Rightarrow {{a}_{T}}=\sqrt{3{{t}^{2}}+\dfrac{9}{16}{{t}^{8}}}\times \cos 60$
$\Rightarrow \sqrt{3}t=\sqrt{3{{t}^{2}}+\dfrac{9}{16}{{t}^{8}}}\times \dfrac{1}{2}$
$\Rightarrow 3{{t}^{2}}=\dfrac{1}{4}\left( 3{{t}^{2}}+\dfrac{9}{16}{{t}^{8}} \right)$
$\Rightarrow \dfrac{9}{16}{{t}^{6}}=9$
$\Rightarrow {{\left( {{t}^{3}} \right)}^{2}}={{\left( {{2}^{2}} \right)}^{2}}$
So, $\Rightarrow t=0$ or $t={{2}^{\dfrac{2}{3}}}$
As $t={{2}^{\dfrac{2}{3}}}$ satisfies the question, the time after which total acceleration of particle makes an angle of $30{}^\circ $ with the radial acceleration is $t={{2}^{\dfrac{2}{3}}}$.

Note:
You can see that we have derived all the required information from the simple acceleration-time graph given in the question. So, in kinematics, one should be able to analyze the graphs properly, otherwise you will not be able to attempt these kinds of questions. Also remember that for any circular motion there will be a centripetal force acting towards the centre and hence a centripetal acceleration.