Question

Take into account the system given in the figure. A pulley and a string are light here, and the surface is frictionless. Then the tension experienced by the string is (Taking $ g = 10\;m/{s^2} $ )
(A) 0N

(B) 1N
(C) 2N
(D) 5N

Answer 1

Hint: When we hear the term tension we must remember that it means force, so its unit will be Newton ( $ N $ ).Identify the areas of the diagram where the tension will appear, a ‘pulling’ force exerted by strings or ropes is called tension. Then note down the equations for motion of the blocks and then combine the equations to calculate tension.

Complete answer:
We know that tension has to be a pulling force because only pull can be exerted by strings or ropes and they cannot exert a push. We need to first identify from the diagram, where exactly the tensions are going to be exerted.
From the diagram we can see that the mass of each of the blocks is $ 1kg $ , and tension by the string should be calculated. We can also see that since the first block is attached to a string but it is kept on a frictionless surface so it will move with an acceleration ‘ $ a $ ’. The second block is attached with a string to the pulley and is hanging, it can move upward with an acceleration ‘ $ a $ ’.

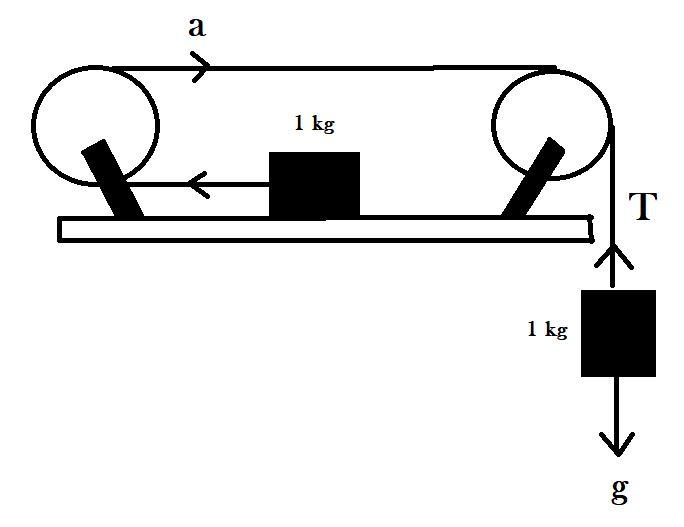
Now we can write the two equations of motion for each block;
For block on the surface: $ T = ma $ $ \to (1) $
For the hanging block: $ T + ma = mg $ $ \to (2) $
The total tension will be adding the equations $ (1) $ and $ (2) $ :
 $ \Rightarrow $ $ 2T + ma = ma + mg $
 $
   \Rightarrow 2T = mg \\
   \Rightarrow T = \dfrac{{1\; \times 10}}{2} \\
   \Rightarrow T = 5N \\
  $ (Since $ m = 1 $ and $ g = 10\;m/s $ )

So the tension exerted by the string in $ 5N $ .
The correct option is (D) 5N.

Note:
By the laws of Physics, we know that when different objects which have different masses are in contact with each other, can apply force. When such a force is applied between objects and one of the objects are certain things like strings, rope, cables or chains, the force exerted is called tension. It is a pull force since a string cannot exert push force.