Question

TA tennis ball is dropped on a horizontal smooth surface. It bounces back to its original position after hitting the surface. The force on the ball during the collision is proportional to the length of compression of the ball. Which one of the following sketches describes the variation of its kinetic energy $ K $ with time $ t $ most appropriately? The figures are only illustrative and not to the scale.
A)

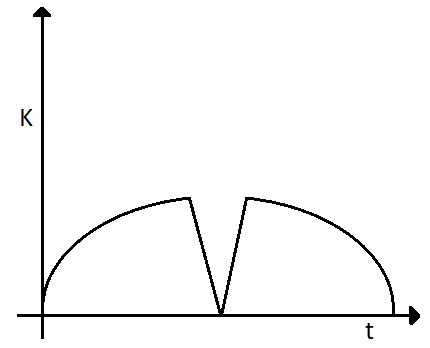
B)

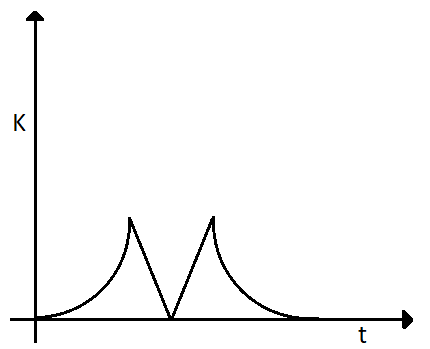
C)

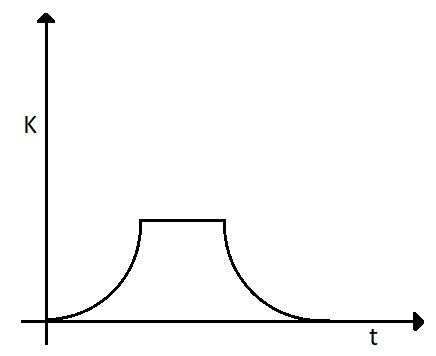
D)

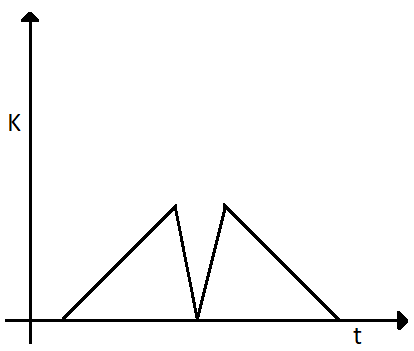
Answer 1

Hint During the first fall, we can find the velocity of the ball before hitting the ground. Using that velocity we can find the kinetic energy and its dependence on time. When it hits the ground, the kinetic energy gets converted to elastic potential energy. Then on leaving the ground the elastic potential energy gets converted to kinetic energy proportionally.

Formula Used: In this solution we will be using the following formula,
 $\Rightarrow v = u + at $
where $ v $ is the final velocity, $ u $ is the initial velocity, $ a $ is the acceleration and $ t $ is the time.

Complete step by step answer
We need to first find the kinetic energy of the ball when it is first dropped to the surface. The ball had no initial velocity and the acceleration of the ball will be given by the acceleration due to gravity.
By using the equation of motion
 $\Rightarrow v = u + at $ , we can substitute $ u $ as zero and the acceleration $ a $ as $ g $ .
Therefore we get,
 $\Rightarrow v = gt $
The kinetic energy of the ball while dropping will be given by the formula,
 $\Rightarrow K = \dfrac{1}{2}m{v^2} $
So substituting the velocity we get,
 $\Rightarrow K = \dfrac{1}{2}m{\left( {gt} \right)^2} $
So we see that the kinetic energy is proportional to $ K \propto {t^2} $
This is the form of the parabola.
After the ball strikes the surface, the kinetic energy converts to the elastic potential energy of the ball in a very small amount of time. The force acting on the ball is like the restoring force on a spring, directly proportional to the displacement.
Then this process reverts back and the elastic potential energy converts to the kinetic energy of the ball again. Now while rising up, the acceleration due to gravity working on the ball will be in a direction opposite to the direction of motion of the ball. So now kinetic energy will be proportional to $ K \propto - {t^2} $
This is also the equation of a parabola.
Therefore, from the above discussion we can conclude that the graph will be

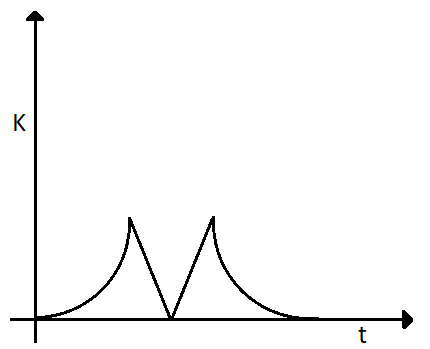
Hence the correct answer is option B.

Note
Here in the case when the ball strikes the surface we have considered that there is no loss in energy in any form. All the kinetic energy of the ball gets converted to the elastic potential energy according to the energy conservation theorem.