Question

T Prove that diagonals of a parallelogram bisect each other.

Answer 1

Hint: For solving this question first we will see some properties of the parallelogram and then prove the result with the help of ASA (Angle Side Angle) congruence rule.

Complete step by step answer:
Given:
We have a parallelogram as shown in the figure below:

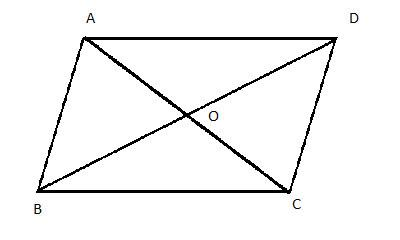
Now, in the above figure in parallelogram ABCD following points should satisfy:
1. AB will be parallel to CD and AD will be parallel to BC.
2. Length of AB = CD and length of AD = BC.
Thus, in a parallelogram opposite sides have equal length and are parallel to each other.
Now, in the above figure:
We can say that, $\angle AOB=\angle DOC$ as they are vertically opposite angles. And $\angle OAB=\angle OCD$ as they are alternate interior angles. Similarly, $\angle OBA=\angle ODC$ as they are alternate interior angles.
Now, in $\Delta AOB$ and $\Delta COD$ . We have:
1. $AB=CD$ ( Opposite sides of the parallelogram are equal).
2. $\angle OAB=\angle OCD$ (Alternate interior angles are equal).
3. $\angle OBA=\angle ODC$ (Alternate interior angles are equal).

Now, by considering the above 3 points with the help of ASA (Angle Side Angle) congruence rule we conclude that: $\Delta AOB\cong \Delta COD$ . As corresponding sides of congruent triangles are equal in length. Then,
$\begin{align}
  & AO=CO..........\left( 1 \right) \\
 & BO=DO...........\left( 2 \right) \\
\end{align}$
Now, as AC and BD are the diagonals of parallelogram ABCD. Using equation (1) and equation (2). Then,
$\begin{align}
  & AO+CO=AC \\
 & \Rightarrow 2AO=AC \\
 & \Rightarrow AO=CO=\dfrac{AC}{2} \\
 & BO+DO=DB \\
 & \Rightarrow 2BO=DB \\
 & \Rightarrow BO=DO=\dfrac{DB}{2} \\
\end{align}$
Now, from the above results, we conclude that O is the midpoint of AC and BD. So, we can say that AC and BD bisects each other at O.
Thus, diagonals of a parallelogram bisect each other.
Hence, proved.

Note: Here, the student must take care of the geometrical properties of the parallelogram. Moreover, be careful in writing the name of congruent triangles. For example in this question we cannot write that $\Delta ABO\cong \Delta DCO$ , the correct way is $\Delta ABO\cong \Delta CDO$ .