Question

T is the point of intersection of tangents drawn at points $P({{t}_{1}})$ and $Q({{t}_{2}})$ of parabola ${{(y+1)}^{2}}=8(x-2)$ and given that ${{t}_{1}}=\dfrac{1}{2}$ and ${{t}_{2}}=1$ . Then the value of $SP.SQ$ where $S$ is the focus is,
(a) 8
(b) 10
(c) 4
(d) 28

Answer 1

Hint: Find the value of $P({{t}_{1}})$ and $Q({{t}_{2}})$ using the parametric form of equation of parabola. If the vertex of the parabola is at $(h,k)$ then generalized form of the parabola is ${{(y-k)}^{2}}=4a(x-h)$ . Its focus is at $(a+h,k)$ and parametric equations are given by $x=h+a{{t}^{2}}$ and $y=k+2at$ . Using ${{(y+1)}^{2}}=8(x-2)$ find the value of coordinates $P({{t}_{1}})$ and $Q({{t}_{2}})$ at ${{t}_{1}}=\dfrac{1}{2}$ and ${{t}_{2}}=1$ . Use the distance formula $\sqrt{{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{x}_{2}}-{{x}_{1}})}^{2}}}$ , where $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$ are the two points in the coordinate plane, to find SP and SQ.

Complete step by step answer:
In the question we are given a parabola ${{(y+1)}^{2}}=8(x-2)$ . We know that generalized equation of parabola is ${{(y-k)}^{2}}=4a(x-h)$ where $(h,k)$ are the vertex of the parabola and its focus is at $(a+h,k)$ and parametric equations are given by $x=h+a{{t}^{2}}$ and $y=k+2at$ . Using this we find that the vertex is at $(2,-1)$ since $a=2$ so focus is at $(4,-1)$.
Using the parametric equations $x=h+a{{t}^{2}}$ and $y=k+2at$ at ${{t}_{1}}=\dfrac{1}{2}$ we will get the coordinates of $P({{t}_{1}})$ , so we have
$\begin{align}
  & {{x}_{1}}=h+a{{t}_{1}}^{2} \\
 & =2+2{{\left( \dfrac{1}{2} \right)}^{2}} \\
 & =\dfrac{5}{2} \\
\end{align}$
And,
$\begin{align}
  & {{y}_{1}}=k+2a{{t}_{1}} \\
 & =-1+(2)(2)\left( \dfrac{1}{2} \right) \\
 & =1 \\
\end{align}$
So the coordinates of P is $P\left( \dfrac{5}{2},1 \right)$ . Similarly we will find the value of the coordinates of $Q({{t}_{2}})$ at ${{t}_{2}}=1$ so we have,
$\begin{align}
  & {{x}_{2}}=h+a{{t}_{2}}^{2} \\
 & =2+2{{\left( 1 \right)}^{2}} \\
 & =4 \\
\end{align}$
And,
$\begin{align}
  & {{y}_{2}}=k+2a{{t}_{2}} \\
 & =-1+(2)(2)\left( 1 \right) \\
 & =3 \\
\end{align}$
Thus the coordinates of Q is $Q(4,3)$ . So the coordinates of P and Q are $P\left( \dfrac{5}{2},1 \right)$ and $Q(4,3)$ . Let the focus of the parabola be S, so the coordinates of focus is $S(4,-1)$ .

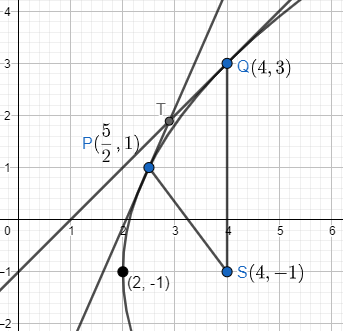
Now we will find the value of SP and SQ by using the distance formula which is $\sqrt{{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{x}_{2}}-{{x}_{1}})}^{2}}}$ where $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$ are the two points in the coordinate plane. Then,
$\begin{align}
  & SP=\sqrt{{{(1-(-1))}^{2}}+{{\left( \dfrac{5}{2}-4 \right)}^{2}}} \\
 & =\sqrt{{{(2)}^{2}}+{{\left( \dfrac{-3}{2} \right)}^{2}}} \\
\end{align}$
After squaring the terms and adding them and then taking the square root we get,
 $\begin{align}
  & =\sqrt{\dfrac{25}{4}} \\
 & =\dfrac{5}{2} \\
\end{align}$
So the value of $SP=\dfrac{5}{2}$ , Similarly we will find the value of SQ.
$\begin{align}
  & SQ=\sqrt{{{(3-(-1))}^{2}}+{{\left( 4-4 \right)}^{2}}} \\
 & =\sqrt{{{(4)}^{2}}+{{\left( 0 \right)}^{2}}} \\
 & =4 \\
\end{align}$
Thus the value of SQ=4. Then the value of SP.SQ is
$\begin{align}
  & (SP)(SQ)=\dfrac{5}{2}\times 4 \\
 & =10 \\
\end{align}$
Hence the value of $SP.SQ=10$ , so option (b) is correct.
Note:
The distance formula is given by $\sqrt{{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{x}_{2}}-{{x}_{1}})}^{2}}}$ where $({{x}_{1}},{{y}_{1}})$ and $({{x}_{2}},{{y}_{2}})$ are the two points in the coordinate plane. The parabola ${{(y+1)}^{2}}=8(x-2)$ has its vertex at $(2,-1)$ , since $a=2$ so focus of the parabola is at $(4,-1)$. We found this value by comparing this parabola with generalized equation of parabola ${{(y-k)}^{2}}=4a(x-h)$ whose focus is at $(a+h,k)$ and vertex is $(h,k)$ .