Question

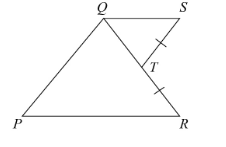
T is a point on the side QR of \[\Delta PQR\]. S is a point such that \[RT = ST\]. Prove that \[PQ + PR > QS\]

Answer 1

Hint: According to the given details in the problem, compare the two triangles \[\Delta PQR\]and \[\Delta QTS\], then prove the sum of the PQ and PR is greater than QS. As we know that a triangle consists of 3 sides and each side has a particular length, so the sum of the two sides of a triangle is greater than the other side of the triangle.

Complete step-by-step answer:
Given:
T is a point on the side QR of\[\Delta PQR\].
S is a point where \[RT = ST\].
According to the given details and the figure, as we know that the sum of the two sides of the \[\Delta PQR\] is greater than the third side, then from triangle \[\Delta PQR\],
\[PQ + PR > QR\]
According to the diagram, the side QR can be written as the sum of QT and QR, it means \[QR = QT + RT\].
\[PQ + PR > QT + RT\]
So, we will substitute QS in place of RT in the above expression, then we get,
\[PQ + PR > QT + TS\,\]…….(1)
Similarly, from triangle \[\Delta QTS\], the sum of the two sides is always greater than the third side, then the equation will become,
\[QT + TS > QS\,\]……….(2)
Then, according to the equation (2), which is taken from the triangle \[\Delta QTS\], the equation (1) can be written as,
\[\begin{array}{l}
PQ + PR > QT + TS\\
PQ + PR > QS
\end{array}\]
Therefore, it is proved that \[PQ + PR > QS\].

Note: In such types of questions, be aware about all the rules as well as properties related to the triangle, while comparing the two triangles \[\Delta PQR\] and \[\Delta QTS\]. Also, try to take the sides that will accurately prove the required equation that is \[PQ + PR > QS\].