Question

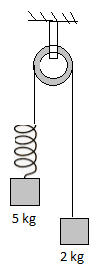
System shown in the figure is released from rest. Pulley and spring are massless and the friction is absent everywhere. The speed of \[5\,{\text{kg}}\] block when \[2\,{\text{kg}}\] block leaves the contact with ground is: (Take force constant of the spring \[K = 40\,{\text{N/m}}\] and \[g = 10\,{\text{m/}}{{\text{s}}^2}\])

A. \[\sqrt 2 \,{\text{m/s}}\]
B. \[2\sqrt 2 \,{\text{m/s}}\]
C. \[2\,{\text{m/s}}\]
D. \[4\sqrt 2 \,{\text{m/s}}\]

Answer 1

Hint: Use the expression for Newton’s second law of motion and determine the displacement of the spring when the 2 kg block leaves its contact with ground. Apply law of conservation of energy to the 5 kg block to determine its velocity when the first 2 kg block leaves the contact with ground.

Formulae used:
The expression for Newton’s second law of motion is
\[{F_{net}} = ma\]
Here, \[{F_{net}}\] is the net force on the object, \[m\] is the mass of the object and \[a\] is the acceleration of the object.
The spring force \[{F_S}\] on the spring is
\[{F_S} = Kx\]
Here, \[K\] is the spring constant and \[x\] is the displacement of the spring.
The kinetic energy \[KE\] of an object is
\[KE = \dfrac{1}{2}m{v^2}\]
Here, \[m\] is the mass of the object and \[v\] is the velocity of the object.
The potential energy \[PE\] of an object is
\[PE = mgh\]
Here, \[m\] is the mass of the object, \[g\] is acceleration due to gravity and \[h\] is the height of the object from ground.

Complete step by step solution:
We have given that there are two blocks 1 and 2 of masses \[2\,{\text{kg}}\] and \[5\,{\text{kg}}\] attached to the pulley and spring respectively.
\[{m_1} = 2\,{\text{kg}}\]
\[{m_2} = 5\,{\text{kg}}\]
The spring constant of the spring is \[40\,{\text{N/m}}\].
\[K = 40\,{\text{N/m}}\]
First, we have to determine the vertical displacement \[y\] of the spring when block 1 leaves the ground.
Initially when the block 1 leaves the contact with ground, the normal force acting on it becomes zero.
Let is the tension in the string of the pulley and the spring in the upward direction.
Apply Newton’s second law to the block 1 in vertical direction.
\[T = {m_1}g\]
Now apply Newton’s second law to the block 2 attached to the spring in a vertical direction.
\[T = {F_S}\]
Substitute \[{m_1}g\] for \[T\] and \[Ky\] for \[{F_S}\] in the above equation.
\[{m_1}g = Ky\]
\[ \Rightarrow y = \dfrac{{{m_1}g}}{K}\]
Substitute \[2\,{\text{kg}}\] for \[{m_1}\], \[10\,{\text{m/}}{{\text{s}}^2}\] for \[g\] and \[40\,{\text{N/m}}\] for \[K\] in the above equation.
\[y = \dfrac{{\left( {2\,{\text{kg}}} \right)\left( {10\,{\text{m/}}{{\text{s}}^2}} \right)}}{{40\,{\text{N/m}}}}\]
\[ \Rightarrow y = 0.5\,{\text{m}}\]
Hence, the displacement of the spring is \[0.5\,{\text{m}}\].
Apply law of conservation of energy to the block attached to the spring.
\[K{E_i} + P{E_i} = K{E_f} + P{E_f}\]
Initially, the kinetic energy of block 2 is zero as it is stationary.
 Hence, the above equation becomes
\[0 + {m_2}gy = \dfrac{1}{2}{m_2}{v^2} + \dfrac{1}{2}K{y^2}\]
\[ \Rightarrow 2gy = {v^2} + \dfrac{{K{y^2}}}{{{m_2}}}\]
\[ \Rightarrow v = \sqrt {2gy - \dfrac{{K{y^2}}}{{{m_2}}}} \]
Substitute \[10\,{\text{m/}}{{\text{s}}^2}\] for \[g\], \[0.5\,{\text{m}}\] for \[y\], \[40\,{\text{N/m}}\] for \[K\] and \[5\,{\text{kg}}\] for \[{m_2}\] in the above equation.
\[ \Rightarrow v = \sqrt {2\left( {10\,{\text{m/}}{{\text{s}}^2}} \right)\left( {0.5\,{\text{m}}} \right) - \dfrac{{\left( {40\,{\text{N/m}}} \right){{\left( {0.5\,{\text{m}}} \right)}^2}}}{{5\,{\text{kg}}}}} \]
\[ \Rightarrow v = \sqrt {10 - 2} \]
\[ \Rightarrow v = \sqrt 8 \]
\[ \Rightarrow v = \sqrt {2 \times 4} \]
\[ \Rightarrow v = 2\sqrt 2 \,{\text{m/s}}\]
Therefore, the velocity of the block is \[2\sqrt 2 \,{\text{m/s}}\].

So, the correct answer is “Option B.

Note:
The tension in both the spring and the string over the pulley are the same and in the upward direction as the spring and pulley are both passing over the same pulley. The final potential energy to the block attached to the spring is provided by the spring potential energy of the spring. Hence, the final potential energy of block 2 is equal to the spring potential energy.