Question

What is the surface area to volume ratio for a cube that measures 4 cm on each side?

Answer 1

Hint: Here in this question, we have to find the ratio between the surface area and volume of a cube. For finding the ratio, firstly we have to find the volume and surface area of cube separately by using the standard formula of cube i.e., \[\text{Volume of cube} = {a^3}\] and \[\text{Surface area of cube} = 6{a^2}\], where a is the measurement side of cube and later by simplifying the ratio to get the required solution.

Complete step by step solution:

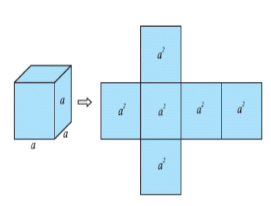
Consider the data in give question
Given cube that measures 4 cm on each side i.e., \[a = 4\,cm\]
Now find the volume of cube with side \[a = 4\,cm\]
The volume of a cube defines the number of cubic units, occupied by the cube completely. A cube is a solid three-dimensional figure, which has 6 square faces or sides. To calculate the volume, we should know the dimensions of the cube.
 \[{\mathbf{Volume}}{\text{ }}{\mathbf{of}}{\text{ }}{\mathbf{a}}{\text{ }}{\mathbf{Cube}}{\text{ }} = {\text{ }}{\mathbf{Length}}{\text{ }} \times {\text{ }}{\mathbf{Width}}{\text{ }} \times {\text{ }}{\mathbf{Height}}\]
 \[V = a \times a \times a\]
 \[V = {a^3}\]
Where ‘a’ is the length of the side of the cube or edges.
In given cube \[a = 4\,cm\] , then
 \[ \Rightarrow V = {4^3}\]
 \[ \Rightarrow V = 64\,c{m^3}\]
Hence, the volume of the cube is \[64\,c{m^3}\] .
Now, find the surface area of the cube with the side \[a = 4\,cm\] .
The surface area of a cube states that the total surface area is equal to the sum of all the areas of the faces of the cube. Since the cube has six faces, therefore, the total surface area of the cube will be equal to the sum of all six faces of the cube, Where ‘a’ is the edge of the cube
 \[{\mathbf{surface}}{\text{ }}{\mathbf{area}}{\text{ }}{\mathbf{of}}{\text{ }}{\mathbf{a}}{\text{ }}{\mathbf{Cube}}{\text{ }}\; = {\text{ }}6{\text{ }} \times {\text{ }}\left( {area{\text{ }}of{\text{ }}each{\text{ }}side} \right)\]
 \[S = 6{a^2}\,c{m^2}\]
In given cube \[a = 4\,cm\] , then
 \[ \Rightarrow S = 6{\left( 4 \right)^2}\,c{m^2}\]
 \[ \Rightarrow S = 6\left( {16} \right)\,c{m^2}\]
 \[ \Rightarrow S = 96\,c{m^2}\]
Hence, the surface area of the cube is \[96\,c{m^3}\] .
To find the ratio of surface area to volume, simply divide the surface area by the volume:
i.e., \[Ratio = \dfrac{{Surface\,area}}{{Volume}}\]
 \[ \Rightarrow Ratio = \dfrac{{96\,c{m^2}}}{{64\,c{m^3}}}\]
On simplification, we get
 \[ \Rightarrow Ratio = 1.5\]
Ratios are generally unit-less but not in our case.
Hence, the ratio of surface area to volume for a cube that measures 4 cm is \[1.5\] per cm .

Note: Generally, for solving this type of questions, we have to know the appearance of different shapes, standard formula of surface area and volume of different shapes and properties of shapes like in cube all sides are the same measurements. And know how to represent the ratio in fraction form.