Question

Suppose you have three concave mirrors A, B and C of focal lengths 10 cm 15 cm and 20 cm. For each concave mirror you perform the experiment of image formation for three values of object distance of 10 cm 20 cm and 30 cm. Giving reason answer the following:
A. For the three object distances identify the mirror/mirrors which will form an image of magnification – 1

Answer 1

Hint: The given question can be solved easily using one key concept. The image formed by the concave mirror for the object kept at the radius of curvature will be of the same size and inverted. So, in other words, magnification will be -1. So, object distance must be equal to 2f.

Complete step-by-step answer:

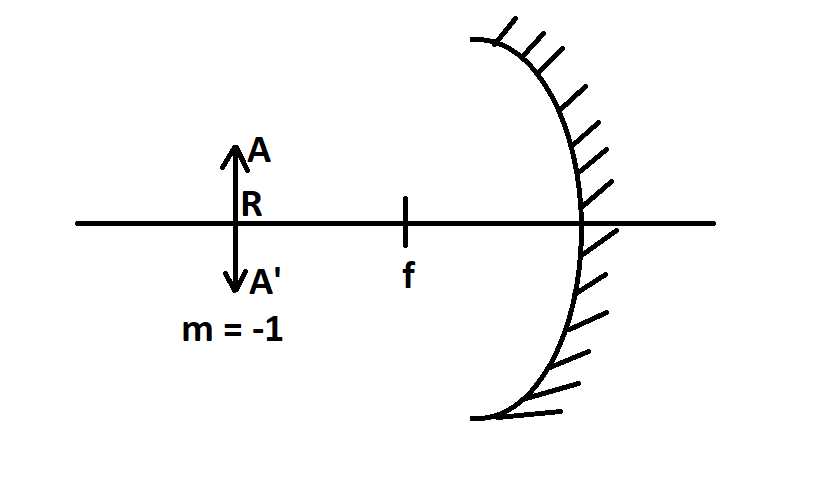
For Mirror A
Now For, m = -1, the object must be placed at the centre of the curvature, that is u =2f
So, now then, At, u = -10 cm, then f must be equal to $\dfrac{u}{2}$ so
$\Rightarrow \dfrac{u}{2}=-\dfrac{10}{2}=5cm$
So it will not be the right object distance for the required magnification,
Again. Then, for u = -20 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{20}{2}=-10cm$
So it will be the right object distance for the required magnification,
Again, for u = -30 cm then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{30}{2}=-15cm$
So it will not be the right object distance for the required magnification

FOR MIRROR B
Now For, m = -1, the object must be placed at the centre of the curvature, that is u =2f
So, now Then, At, u = -10 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{10}{2}=5cm$
So it will not be the right object distance for the required magnification,
Again. Then, for u = -20 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{20}{2}=-10cm$
So it will be not the right object distance for the required magnification,
Again, for u = -30 cm then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{30}{2}=-15cm$
So, it will be the right object distance for the required magnification

FOR MIRROR C
Now, For, m = -1, the object must be placed at the centre of the curvature, that is u =2f
So, now Then, At, u = -10 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{10}{2}=5cm$
So it will not be the right object distance for the required magnification,
Again.Then, for u = -20 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{20}{2}=-10cm$
So it will be the right object distance for the required magnification,
Again, for u = -30 cm, then f must be equal to $\dfrac{u}{2}$
$\Rightarrow \dfrac{u}{2}=-\dfrac{30}{2}=-15cm$
So it will not be the right object distance for the required magnification
So, we can say that for the mirror A, the desired object distance will be 20 cm, and for the mirror B it will 30 cm. whereas, for the mirror C the given set of object distances wll not give the desired result

Note: Sign convention is a set of guidelines for mathematical study of image creation to set signs for image distance, object distance, focal length, etc. It's according to:
1. Objects are typically located to the left of the mirror
2. From the pole of the mirror, all lengths are determined.
3. The distances measured are positive in the direction of the incident ray, and the distances measured are negative in the direction opposite to that of the incident ray.
4. Distances measured above the main axis along the y-axis are positive, and those measured below the main axis along the y-axis are negative.