Question

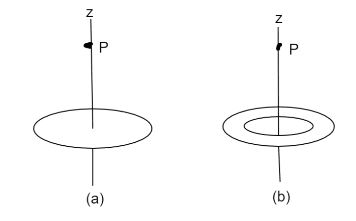
Suppose you design an apparatus in which a uniformly charged disk of radius \[R\] is to produce an electric field. The field magnitude is most important along the central perpendicular axis of the disk, at a point $P$ at distance $2.00R$ from the disk. Cost analysis suggests that you switch to a ring of the same outer radius $R$ but with inner radius $\dfrac{R}{{2.00}}$. Assume that the ring will have the same surface charge density as the original disk. If you switch to the ring, by what percentage will you decrease the electric field magnitude at $P$ ?

Answer 1

Hint: Let the electric field produced by the disc in figure (a) be ${E_a}$ and the electric field produced by the disc in figure (b) be ${E_b}$ . Find ${E_a}$. We can see that the disc given in (a) is similar to (b) but there is an inner ring which will also produce an electric field . so ${E_b}$ will be equal to ${E_a}$ minus the electric field produced by the inner ring. Finally to find the decrease in the electric field, find the difference between ${E_a}$ and ${E_b}$ then divide it by the original electric field ${E_a}$.

Complete step by step answer:
we know the electric field due to a charged electric field is equal to,
$E = \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{z}{{\sqrt {{z^2} + {R^2}} }}} \right)$
Here, $\sigma $ is the surface charge density, ${\varepsilon _0} = 8.85 \times {10^{ - 12}}\,C^2/Nm^2$ is the permittivity of free space, $R$ is the radius of the disc and $z$ is the distance from the centre of the disc to the point $P$.

Let electric field at point $P$ in the given figure (a) be
${E_a} = \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{z}{{\sqrt {{z^2} + R{}^2} }}} \right)$
$ \Rightarrow {E_a} = \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{{2R}}{{\sqrt {{{\left( {2R} \right)}^2} + {R^2}} }}} \right)$
$ \Rightarrow {E_a} = \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{{2R}}{{\sqrt {5{R^2}} }}} \right)$
$ \Rightarrow {E_a} = \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{2}{{\sqrt 5 }}} \right)$
Now disc in figure (a) is equal to disc in figure (b) but there is an inner ring with radius $\dfrac{R}{2}$ in figure (b) which will also produce some electric field, so we have to subtract that.

Therefore electric field at point $P$ in the given figure (b) be
${E_b} = {E_a} - \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{{2R}}{{\sqrt {{{\left( {2R} \right)}^2} + {{\left( {\dfrac{R}{2}} \right)}^2}} }}} \right)$
$ \Rightarrow {E_b} = {E_a} - \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{{2R}}{{\sqrt {\dfrac{{17}}{4}{R^2}} }}} \right)$
$ \Rightarrow {E_b} = {E_a} - \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{2}{{\sqrt {\dfrac{{17}}{4}} }}} \right)$
Now the decrease in the electric field at point $P$ will be
$E' = \dfrac{{{E_a} - {E_b}}}{{{E_a}}}$
\[ \Rightarrow E' = \dfrac{{{E_a} - {E_a} + \dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{2}{{\sqrt {\dfrac{{17}}{4}} }}} \right)}}{{\dfrac{\sigma }{{2{\varepsilon _0}}}\left( {1 - \dfrac{2}{{\sqrt 5 }}} \right)}}\]
Solving this we will get
$\therefore E' = 0.283$

Hence, the percentage you will decrease the electric field magnitude at $P$ is $28.3\% $.

Note: Charge density is the quantity of electric charge per unit length, surface area, or volume in electromagnetism that is the amount of electric charge deposited in a certain field. Based on the dimensions provided, it determines the quantity of electric charge.