Question

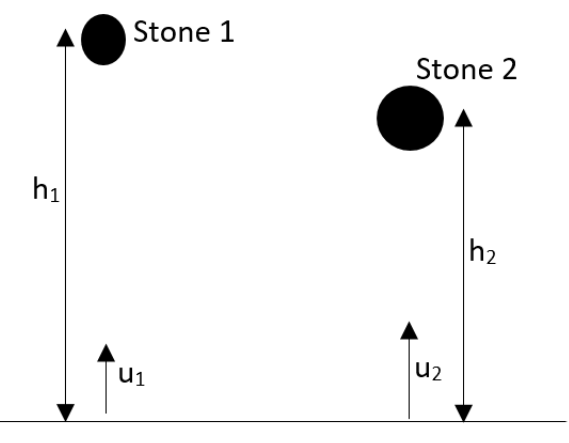
Suppose that two stones have been simultaneously thrown vertically upwards with initial velocities mentioned as ${{u}_{1}}$ and ${{u}_{2}}$. Prove that the ratio of the heights reached by them will be $\dfrac{{{u}_{1}}^{2}}{{{u}_{2}}^{2}}$.

Answer 1

Hint: Find out the initial velocity and final velocity of both the stones. Then apply the third equation of motion. The square of the final velocity will be equivalent to the sum of the square of the initial velocity and the product of the twice the acceleration and the displacement. This will help you in answering the question.

Complete step by step answer:
First of all let us consider the first stone. For the first stone, the initial velocity is given as
$u={{u}_{1}}$
And the final velocity will be zero as at maximum heights, the stone will be at rest. That is,
$v=0$
The newton’s third equation of motion is mentioned as,
${{v}^{2}}-{{u}^{2}}=2as$
Where $a$ be the acceleration due to gravity mentioned as,
$a=-g$
$s$ be the displacement or height of the stone. This can be shown as,
$s={{h}_{1}}$
Substituting the values in it will give,
\[\Rightarrow {{0}^{2}}-{{u}_{1}}^{2}=2\times \left( -g \right)\times {{h}_{1}}\]
That is,
\[\Rightarrow {{h}_{1}}=\dfrac{{{u}_{1}}^{2}}{2g}\]…….. (1)
Similarly for the second stone,
The initial velocity is given as
$u={{u}_{2}}$
And the final velocity will be zero as at maximum heights, the stone will be at rest. That is,
$v=0$
The newton’s third equation of motion is mentioned as,
${{v}^{2}}-{{u}^{2}}=2as$
Where $a$ be the acceleration due to gravity mentioned as,
$a=-g$
$s$ be the displacement or height of the stone. This can be shown as,
$s={{h}_{2}}$
Substituting the values in it will give,
\[\Rightarrow {{0}^{2}}-{{u}_{2}}^{2}=2\times \left( -g \right)\times {{h}_{2}}\]
That is,
\[\Rightarrow {{h}_{2}}=\dfrac{{{u}_{2}}^{2}}{2g}\]…….. (2)
Taking the ratio of equation (1) and (2) will give,
\[\begin{align}
  & \dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{\dfrac{{{u}_{1}}^{2}}{2g}}{\dfrac{{{u}_{2}}^{2}}{2g}} \\
 & \Rightarrow \dfrac{{{h}_{1}}}{{{h}_{2}}}=\dfrac{{{u}_{1}}^{2}}{{{u}_{2}}^{2}} \\
\end{align}\]

Hence proved.

Note: Velocity is the rate of variation of displacement of the body. Velocity is found to be a vector quantity. And also the displacement of the object is described as the shortest distance between the initial and final positions of the body.