Question

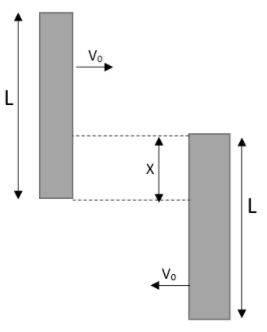
Suppose that two identical rigid rods, each of mass $1kg$ and length $3m$ are moving exactly opposite to each other without rotation on a smooth horizontal table. What will be the maximum value of $X$ after rounding off? Note that the direction of motion of each rod would not change after collision irrespective of the type of collision. Let us assume that there is no sticking.

Answer 1

Hint: In this question, the momentum will be conserved for the system. First of all calculate the momentum conservation. The torque of the rotation is found by taking the product of the distance and the force acting. This will be equal to the product of the moment of inertia and the angular velocity of the body. This all will help you in answering this question.

Complete answer:
According to the momentum conservation, we can write that,
$\int{N\cdot dt=M\left( V-{{V}_{0}} \right)}$……………. (1)
Where $N$be the normal force, \[M\] be the mass, \[V,{{V}_{0}}\]are the velocities respectively.
Here the torque will be equal to,
$\int{Ndt\cdot \left( \dfrac{L}{2}-\dfrac{X}{2} \right)=I\omega }$
As we all know, the moment of inertia of a rigid rod is given as,
\[I=\dfrac{M{{L}^{2}}}{12}\]
Substituting this in the equation will give,
$\int{Ndt\cdot \left( \dfrac{L-X}{2} \right)=\dfrac{M{{L}^{2}}}{12}\omega }$…………………. (2)
And also we know that the velocity is given as,
$v=r\omega $
Let us take the coefficient of restitution,
$e=\dfrac{\omega \left( \dfrac{L-X}{2} \right)-V}{{{V}_{0}}}$……………….. (3)
Let us divide the equation (1) and (2) now. That is,
$\dfrac{L-X}{2}=\dfrac{{{L}^{2}}\omega }{12\left( V-{{V}_{0}} \right)}$
This can be substituted in the equation (3) which can be written as,
\[e{{V}_{0}}=\left( \dfrac{L-X}{2}\times \dfrac{12\left( V-{{V}_{0}} \right)}{{{L}^{2}}} \right)\dfrac{L-X}{2}-V\]
Expanding the bracket will give,
\[e{{V}_{0}}=\left( {{\left( \dfrac{L-X}{2} \right)}^{2}}\times \dfrac{12\left( V-{{V}_{0}} \right)}{{{L}^{2}}} \right)-V\]
Taking \[{{V}_{0}}\] as common and rearranging the equation in terms of it will give,
\[{{V}_{0}}\left( e+12{{\left( \dfrac{L-X}{2L} \right)}^{2}} \right)=V\left[ 12{{\left( \dfrac{L-X}{2L} \right)}^{2}}-1 \right]\]
Rearranging this equation will give,
$X=L+\sqrt{\dfrac{{{L}^{2}}}{3}\left( \dfrac{{{V}_{0}}e+V}{V-{{V}_{0}}} \right)}$
That is,
${{X}_{\max }}=3+\sqrt{\dfrac{{{3}^{2}}}{3}\left( \dfrac{{{V}_{0}}e+V}{V-{{V}_{0}}} \right)}=3+\sqrt{3\left( \dfrac{{{V}_{0}}e+V}{V-{{V}_{0}}} \right)}$
Therefore the answer has been obtained.

Note:
Moment of inertia otherwise known as angular inertia is a characteristic of a rotating body with respect to its rotation. It is the opposition of the rotating body to angular acceleration or deceleration. This is found to be equal to the product of the mass and the square of its perpendicular distance from the axis of rotation.