Question

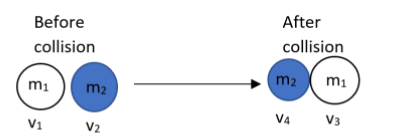
Suppose that a body of mass ${{m}_{1}}$ is in motion having an unknown velocity of ${{V}_{1}}\hat{i}$, is undergoing a collinear collision with a body of mass ${{m}_{2}}$​ moving with a velocity ${{V}_{2}}\hat{i}$. The mass ${{m}_{1}}$​ and ${{m}_{2}}$ move with velocities of ${{V}_{3}}\hat{i}$ and ${{V}_{4}}\hat{i}$, respectively after the collision. If ${{m}_{2}}=0.5{{m}_{1}}$​ and ${{V}_{3}}=0.5{{V}_{1}}$​, then ${{V}_{1}}$ will be given as,
\[\begin{align}
  & A.{{V}_{4}}-\dfrac{{{V}_{2}}}{4} \\
 & B.{{V}_{4}}-\dfrac{{{V}_{2}}}{2} \\
 & C.{{V}_{4}}-{{V}_{2}} \\
 & D.{{V}_{4}}+{{V}_{2}} \\
\end{align}\]

Answer 1

Hint: The linear momentum is conserved in this situation mentioned in the question. It means that the initial momentum will be equivalent to the final momentum. A momentum is defined as the product of mass of the body and it’s velocity of the body. This will help you in answering this question.

Complete step by step answer:
First of all, let us mention what all are given in the question. The mass of the first body is given as ${{m}_{1}}$. The velocity of this body is mentioned as ${{V}_{1}}$. The mass of the second particle is mentioned as ${{m}_{2}}$. The velocity of this body is mentioned as ${{V}_{2}}\hat{i}$. After the collision the velocity of the first body is given as ${{V}_{3}}\hat{i}$ and the same of the second body is mentioned as ${{V}_{4}}\hat{i}$.
It has been mentioned that the relation between the mass is mentioned in the question as,
${{m}_{2}}=0.5{{m}_{1}}$
And the relation between the velocity is given as,
${{V}_{3}}=0.5{{V}_{1}}$
As we all know, the conservation of linear momentum is given as the initial momentum will be equivalent to the final momentum.
That is,
\[{{m}_{1}}{{V}_{1}}\hat{i}+{{m}_{2}}{{V}_{2}}\hat{i}={{m}_{1}}{{V}_{3}}\hat{i}+{{m}_{2}}{{V}_{4}}\hat{i}\]
Applying the relations mentioned in the question as,
\[{{m}_{1}}{{V}_{1}}+0.5{{m}_{1}}{{V}_{2}}={{m}_{1}}\left( 0.5{{V}_{1}} \right)+0.5{{m}_{1}}{{V}_{4}}\]
Simplifying this equation will give,
\[0.5{{m}_{1}}{{V}_{1}}=0.5{{m}_{1}}\left( {{V}_{4}}-{{V}_{2}} \right)\]
From this we can derive the equation of the velocity as,
\[{{V}_{1}}=\left( {{V}_{4}}-{{V}_{2}} \right)\]
Therefore the velocity of the first particle has been obtained. Therefore the correct answer is mentioned as option C.

Note:
The law of conservation of momentum states that the total momentum of a closed system remains constant. This law has a great relation with Newton's law of motion. The Noether’s theorem is used to prove the law of conservation of momentum.