Question

Suppose in a right triangle, $\cos (t) = \dfrac{3}{4}$. How do you find: $\cot (t)$?

Answer 1

Hint: We will use the fundamental equation,
${\sin ^2}(t) + {\cos ^2}(t) = 1$
We can deduce the $\sin (t)$. And then, find the value of $\sin (t)$ .
After that, we substitute the values of $\sin (t)$ and $\cos (t)$ in the equation, i.e.,
$\cot (t) = \dfrac{{\cos (t)}}{{\sin (t)}}$ .
Hence, we will get the required answer.

Complete step by step answer:
We have been given the following trigonometric ratio,
$\cos (t) = \dfrac{3}{4}$
We know that fundamental equation is,
${\sin ^2}(t) + {\cos ^2}(t) = 1$
We can deduce the value of $\sin (t)$ using this equation. At first, we will shift all the values to the right-hand side, such that only that ratio remains on the left-hand side, which is to be found.
${\sin ^2}(t) = 1 - {\cos ^2}(t)$
Now, we will square root both the sides.
$\sin (t) = \pm \sqrt {1 - {{\cos }^2}(t)} $
So, we substitute the value of $\cos (t)$in the equation,
\[\sin (t) = \pm \sqrt {1 - {{\left( {\dfrac{3}{4}} \right)}^2}} \]
Now squaring the term of $\dfrac{3}{4}$ , we will get,
$\sin (t) = \pm \sqrt {1 - \dfrac{9}{{16}}} = \pm \sqrt {\dfrac{{16 - 9}}{{16}}} $
Subtract the numerator term,
$\sin (t) = \pm \sqrt {\dfrac{7}{{16}}} $
Now, we have the value of $\sin (t)$
Since $t$ is an angle of a right triangle; the inner angles of a triangle sum to $\pi $, but since one angle is right, the other two must sum to $\dfrac{\pi }{2}$ , and thus they are acute.
Hence the choice of the sign will be affected, since an acute angle lies in the first quadrant, where both sine and cosine are positive, we will discard $\sin (t) = - \sqrt {\dfrac{7}{{16}}} $ .
Now we know both sine and cosine, we compute the cotangent,
$\cot (t) = \dfrac{{\cos (t)}}{{\sin (t)}}$
$\cot (t) = \dfrac{{\dfrac{3}{4}}}{{\dfrac{{\sqrt 7 }}{4}}}$
Now divide the term is, we get
$\cot (t) = \dfrac{3}{4} \cdot \dfrac{4}{{\sqrt 7 }}$
The common term of numerator and denominator reduces, hence we get
$\cot (t) = \dfrac{3}{{\sqrt 7 }}$

Then, the value of $\cot (t)$ is $\dfrac{3}{{\sqrt 7 }}$ .

Note: We can use the Pythagorean theorem and properties of sine, cosines and tangents to solve the triangle.

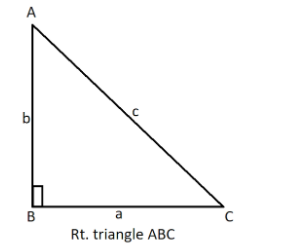
Pythagorean theorem: ${a^2} + {b^2} = {c^2}$.
Look at the figure shown.
Sine: $\sin A = \dfrac{a}{c},\sin B = \dfrac{b}{c}$ .
Cosine: $\cos A = \dfrac{b}{c},\cos B = \dfrac{a}{c}$.
Tangents: $\tan A = \dfrac{a}{b},\tan B\dfrac{b}{a}$ .
This is how we can use the right triangle to solve the question.