Question

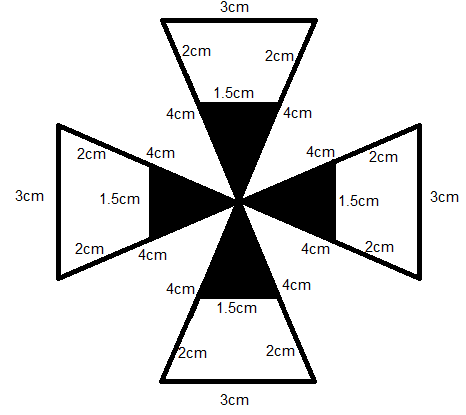
Suman made an arrangement with white and black coloured paper sheets as shown in figure. The total area of white and black paper sheets used in making the arrangement is $15c{m^2}$.

Answer 1

Hint: We can consider one triangle. Then we can find its perimeter by taking the sum of the sides and then the semi perimeter by dividing the perimeter with 2. Then we can find the area of the triangle using the equation $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $. Then we can multiply the area of one triangle with 4 to get the area of the total paper used.

Complete step-by-step answer:
We need to find the total area of white and black paper sheets.
From the figure, we understand that each triangle is made up of white and black sheets. So we need to find the area of the 4 triangles.

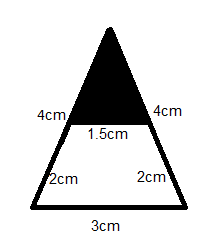
From the measurements, we can say that the area of the 4 triangles are equal. So, we can find the area of one triangle and multiply it with 4 to get the total area.
We know that area of a triangle when the lengths of the sides are given is given by the equation, $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ where s is the semi perimeter and a, b and c are the sides of the triangle.
From the figure, the perimeter of the triangle is given by,
$P = 3 + 4 + 4$
$ \Rightarrow P = 11$
We know that the semi perimeter is the half of the perimeter.
$ \Rightarrow s = \dfrac{P}{2}$
$ \Rightarrow s = \dfrac{{11}}{2}$
$ \Rightarrow s = 5.5$
Now we can find the area,
$ \Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
On substituting the values, we get,
$ \Rightarrow A = \sqrt {5.5\left( {5.5 - 4} \right)\left( {5.5 - 4} \right)\left( {5.5 - 3} \right)} $
On simplification, we get,
$ \Rightarrow A = \sqrt {5.5\left( {1.5} \right)\left( {1.5} \right)\left( {2.5} \right)} $
On taking the products, we get,
$ \Rightarrow A = \sqrt {30.9375} $
On taking the square root, we get,
$ \Rightarrow A = 5.56c{m^2}$
Now we can find the total area.
$ \Rightarrow Area = 4A$
$ \Rightarrow Area = 4 \times 5.56$
$ \Rightarrow Area = 22.24c{m^2}$
So, the total area of the paper used is $22.24c{m^2}$
It is given that the total area of white and black paper sheets used in making the arrangement is $15c{m^2}$.
So, the given statement is false.
So, the correction answer is option B.

Note: Alternate method to find the area of the triangle is by,

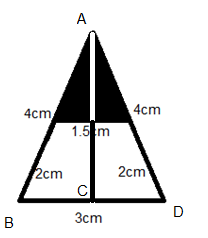
Consider one triangle. From the measurements of the sides, we can say that the triangle is isosceles.
Then by properties of isosceles triangles AC is the perpendicular bisector of BD.
\[ \Rightarrow BC = CD = \dfrac{{BD}}{2}\]
\[ \Rightarrow BC = CD = \dfrac{3}{2}\]
\[ \Rightarrow BC = CD = 1.5cm\]
Now we can consider the right-angled triangle ACD. On applying Pythagoras theorem, we get,
$A{D^2} = C{D^2} + A{C^2}$
On substituting the values, we get,
$ \Rightarrow {4^2} = {1.5^2} + A{C^2}$
$ \Rightarrow 16 = 2.25 + A{C^2}$
$ \Rightarrow A{C^2} = 16 - 2.25$
$ \Rightarrow A{C^2} = 13.75$
In taking square root, we get,
$ \Rightarrow AC = \sqrt {13.75} $
$ \Rightarrow AC = 3.708$
Now we have the height of the triangle, so the area of triangle is given by,
$A = \dfrac{1}{2} \times AC \times BD$
On substituting the values, we get,
$ \Rightarrow A = \dfrac{1}{2} \times 3.708 \times 3$
$ \Rightarrow A = 5.56c{m^2}$
Now we can find the total area.
$ \Rightarrow Area = 4A$
$ \Rightarrow Area = 4 \times 5.56$
$ \Rightarrow Area = 22.24c{m^2}$
So, the total area of the paper used is $22.24c{m^2}$