Question

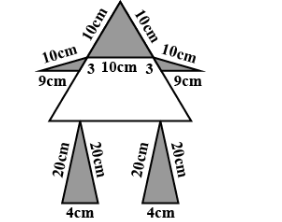
Suman made a picture with some white paper and a black paper as shown in figure. White paper is available at her home and free of cost. The cost of black paper used is at the rate of $ 10 $ paise per $ {\text{c}}{{\text{m}}^2} $ , then the total cost of the black paper used. (Take \[\sqrt 3 = 1.732\;{\text{and}}\;\sqrt {11} = 3.31\]) is Rs. $ 14.92 $
A.True
B.False

Answer 1

Hint: To choose the correct option, you have to find the price of black paper used in making the picture. To find the price, first find the area of the black paper used by finding the areas of all triangles and then adding them. And then multiply the area with the given rate to find the price.

Complete step-by-step answer:
In order to find whether the price given is true or false, we have to find the price of black paper used in making the picture. So we will first find the area of black paper used and for that we will find individual triangle areas and then sum-up them.
Area of equilateral triangle with sides $ 10{\text{cm,}}\;{A_1} = \dfrac{{\sqrt 3 }}{4} \times {10^2} = 25\sqrt 3 = 25 \times 1.732 = 43.3{\text{c}}{{\text{m}}^2} $
Now, area of triangles with sides \[10{\text{cm,}}\;9{\text{cm}}\;{\text{and}}\;{\text{3cm}}\] can be calculated by Heron’s formula,
 $
  s = \dfrac{{10 + 9 + 3}}{2} = 11{\text{cm}} \\
  {A_2} = \sqrt {11 \times (11 - 10) \times (11 - 9) \times (11 - 3)} = \sqrt {11 \times 1 \times 2 \times 8} = 4\sqrt {11} = 4 \times 3.31 = 13.24{\text{c}}{{\text{m}}^2} \;
  $
Similarly for the triangles with sides \[20{\text{cm,}}\;20{\text{cm}}\;{\text{and}}\;4{\text{cm}}\]
 $
  s = \dfrac{{20 + 20 + 4}}{2} = 22{\text{cm}} \\
  {A_3} = \sqrt {22 \times (22 - 20) \times (22 - 20) \times (22 - 4)} = \sqrt {22 \times 2 \times 2 \times 18} = 12\sqrt {11} = 12 \times 3.31 = 39.72{\text{c}}{{\text{m}}^2} \;
  $
Therefore total area of black paper,
\[
   = {A_1} + 2{A_2} + 2{A_3} \\
   = 43.3 + 2 \times 13.24 + 2 \times 39.72 \\
   = 149.22 \;
 \]
So its cost will be $ = 149.22 \times 10 \times \dfrac{1}{{100}} = Rs.14.92 $
Therefore the right cost of black paper is given, that is true.
So, the correct answer is “Option A”.

Note: This type of questions, where you will face to find the area of a discrete parts of a figure, first of all figure out different symmetric shapes from it and also polynomials so that you can find their areas with help of available formulae and eventually the area of whole.