Question

Sum of two sides of a triangle is …………. than the third side.
(A). Greater
(B). Lesser
(C). Equal
(D). May be greater or lesser

Answer 1

Hint- In order to deal with this question first we will make a diagram then by extending the side of a triangle we will use the property of isosceles triangle, use this property to get the answer.

Complete step-by-step answer:

Let ABC be a triangle

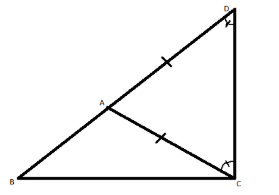
We can extend BA past A into a straight line.
Then there is a point D such that DA = CA
Therefore, from isosceles triangle has two equal angles,
$\angle ADC = \angle ACD$
Thus, in $\Delta DCB,$
$\angle BCD > \angle BDC{\text{ }}\left[ {{\text{side opposite greater angle is larger}}} \right]$
Thus,
$
  BD > CD \\
  BA + AD > CD{\text{ }}\left[ {{\text{since, AC = AD}}} \right] \\
  BA + AC > CD \\
$
The sum of any two sides of the triangle is greater than the third side and the correct option is “A”.

Note- In order to solve these types of questions, remember the theorems and properties of triangles. Also the concept of parallel line and angles. To prove the above theorem we use the isosceles triangle. We can also take an equilateral triangle to prove as we know that all sides of the equilateral triangle are equal therefore the sum of two sides is twice the third side. Hence, the sum of two sides of the triangle is greater than the third side.